
Hugh 'Ras' Riddle: I didn't see it as significant as I do now.
Tony Pritchett: I didn't think of it that way either. I thought - this is fun!
Tony Pritchett created The Flexipede in 1967, probably the first known character computer animation telling a story worldwide, certainly in the UK. And it had a soundtrack.

Sadly, Tony Pritchett passed away on the 28 August 2017.
Animator and filmmaker Kate Sullivan was a friend of Tony’s. She is currently creating a multimedia project which documents his work. The pair were working on the project together at the time of his passing.
Kate is providing a temporary home for Tony’s archive. The collection includes all sorts of fascinating materials relating to his animation career, (1967 – 1982). Items include, the original 16mm master negative of ‘The Flexipede’ along with film footage and printed materials relating to a wide range of projects, (Ridley Scott’s ‘Alien’, ‘Blade Runner’ and the very first Channel Four logo to name but a few.)
Kate is very keen to hear from any one who would like to contribute to the project, which is currently in progress. It is centred upon Tony’s career, but by extension documents the work of his colleagues and the formative years of the British computer animation industry. All contributions would be very much appreciated. No contribution is either too anecdotal or technical! If you would like to get in touch or simply find out more about the project-in-progress, please visit; it’s (regularly-updated) home: http://www.TonyPritchett.co.uk/.
Back in the archive - Kate mentioned to Victoria Marshall that amongst Tony's possessions was a 2000-card drawer of computer punched-cards cards which, according to Tony, included his Flexipede program. Would it be possible to recreate The Flexipede 50 years after it was written?

The card box included several card decks destined for the London Atlas Computing Service. Most cards had printing across the top, rather faded at times. Some had no printing. It was then necessary to read the hole punching.

An early deck that we looked at appeared to be Flexipede but it was an earlier version. Kate has some experimental 16mm footage containing this version. Other decks were from other animation projects.
Eventually, a card deck was found that looked correct. It was generating an IBM-compatible magnetic tape for the Benson-Lehner 120 (BL120) Microfilm Recorder at Culham Laboratory (where Tony Pritchett said the film was produced).
In the 1960s, the sensible way to generate computer animation was to use a microfilm recorder. A Stromberg-Carlson 4020 (SC4020) microfilm recorder was installed at AWRE Aldermaston in 1963 and was also used by Harwell for displaying nuclear simulations on hardcopy paper or 16mm/35mm film. In 1965 thermonuclear research moved from Harwell to Culham, who purchased a BL120 microfilm recorder (compatible with the SC4020). The BL120 was a faster cheaper second-generation alternative that could process all SC4020 magnetic tapes.
Kate Sullivan took on the mammoth job of photographing the box of cards, 3 cards per photograph. Bob Hopgood typed in the contents (making quite a few errors in the process) and David Duce produced a Java program that performed as close to the Fortran program as possible generating frames of SVG graphics that could be displayed approaching 24 frames per second to simulate the BL120 output. This uncovered quite a few errors in the card transcriptions that needed to be addressed.
Only two cards of the deck were missing and we were able to deduce these to arrive at a complete listing of the card deck:
JOB
LRF91PB1, A PRITCHETT BL120 TEST
INPUT
1 LEAP TRAJECTORY
2 WALK TABLE
OUTPUT
0 LINEPRINTER 2000 LINES
13 ANY 100 LINES
STORE 50/120 BLOCKS
TAPE
1 BL L0454*INHIBIT
TAPE IBM
14 LP099*PERMIT 556 DENSITY
COMPUTING 5 MINUTES
COMPILER FORTRAN
*RUN
*FORTRAN SOURCE
*LIBRARY TAPE 1 BLOCK 1
BEGIN
LM=12
NS=11
NAM=24
BEGIN
DIMENSION XK(NS,NAM),YK(NS,NAM),XFT(NS,NAM),YFT(NS,NAM),XBOD(NS)
READ(2,2) XFT,YFT,XK,YK,XBOD
2 FORMAT(1X,11F7.1)
C
YSKULL=0
YJAW=0
C
INTEGER XS,YS,XF,YF
REAL XSFTA,YSFTA,SBOT
PI=3.1416
PITCH=100
D=48
DX=8
BB=19600
DXSOL=40
DFT=6
C
C SET UP SOLIPEDE
DIMENSION YSOL(LM),XSFT(LM),YSFT(LM),XKS(LM),YKS(LM)
C
DO (SETUP) L=1,LM
C
READ(1,1) YSOL(L),YSFT(L)
1 FORMAT(2F5.0)
C
IF(YSFT(L)=0) XSFT(L)=DXSOL*(L-1)
IF(YSFT(L).NE.0) XSFT(L)=XSFT(L-1)+DFT
C
AY=YSOL(L)-YSFT(L)
AA = XSFT(L)**2 + AY**2
A = SQRT(AA)
C = SQRT(BB-AA)
XKSL(L) = (C*AY/A+XSFT(L))/2
YKSL(L) = (AY - C*XSFT(L)/A)/2
C
SETUP CONTINUE
C
C PICTURE ARRAYS
REAL (BODY(2,4)/
1 50., 5.,
2 -50., -5.,
3 -50.,205.,
4 50.,195./
NBODY=4
REAL SOLIBOD(2,5)/
1 50.,5.,
2 -50.,-5.,
3 -50.,205.,
4 50.,195.,
5 50.,5./
NSOLIBOD=5
REAL FOOT(2,4)/
1 0.,0.,
2 0.,-10.,
3 40.,-10.,
4 0.,0./
NFOOT=4
REAL SKULL(2,5)/
1 50.,30.,
2 50,.205.,
3 150.,195.,
4 230.,30.,
5 50.,30./
NSKULL=5
REAL DJAW(2,5)/
1 50.,30.,
2 210.,30.,
3 160.,0.,
4 50.,-10.,
5 50.,30./
NJAW=5
REAL EYE(2,8)/
1 150.,140.,
2 120.,140.,
3 120.,170.,
4 150.,170.,
5 150.,150.,
6 130.,150.,
7 130.,160.,
8 140.160./
NEYE=8
REAL PAD(2,11)/
1 -25.,50.,
2 -25.,30.,
3 -20.,20.,
4 -10.,12.,
5 -3.,10.,
6 0.,10.,
7 0.,70.,
8 -3.,70.,
9 -10.,68.,
/ -20.,60.,
1 -25,50./
NPAD=11
C
REAL PL(4,4)/
1 50.,50.,90.,110.,
2 66.,25.,120.,70.,
3 69.,10.,136.,30.,
4 70.,0.,140.,6./
C
C MAIN PROGRAM
C
CALL IDST
C
NS=10
L=1
NEYE=2
NA=1
C
C 1)FCROSS
SCALE=0.5
INVX=0
GRND=903
BOT=GRND+120
XHEAD=-240
NF=420
CALL FLEXIGO
C
NF=24
CALL BLANK
C
C 2)SCROSS
SCALE=0.2
INVX=1
SGRND=3250
XSOL=-50
NF=150
CALL SOLIHOP
C
NF=24
CALL BLANK
C
C 3)FCROSS
SCALE=0.75
INVX=1
GRND=420
BOT=GRND+120
XHEAD=-240
NF=100
CALL FLEXIGO
C
C 4)F STOPS, S APPEARS
SGRND=2000
XSOL=-1000
NF=120
NEYE=8
C
DO(SPY) M=1,NF
CALL ADVFLM(1)
SCALE=0.75
INVX=1
CALL FLEXIPEDE
SCALE=0.3
INVX=0
CALL LEAP
SPY CALL SOLIPEDE
C
C 6) F CONTINUES
SCALE=0.75
INVX=1
NEYE=2
NF=300
CALL FLEXIGO
C
NF=24
CALL BLANK
C
C 7) S FINAL CROSS
SCALE=1
INVX=1
SGRND=296
XSOL=-50
NF=30
CALL SOLIHOP
C
NF=24
CALL BLANK
C
C MEET
GRND=296
SGRND=GRND
BOT=GRND+120
XSOL=-190
XHEAD=-250
YSKULL=20
SCALE=1
INVX=0
L=10
NMEET=14
C
DO(MEET) N=1,NMEET
CALL ADVFLM(1)
CALL LEAP
CALL SOLIPEDE
MEET CONTINUE
C
C GRAB
XTONG=200
CALL ADVFLM(1)
CALL LEAP
CALL SOLIPEDE
CALL TONGUE
CALL ADVFLM(1)
CALL LEAP
CALL SOLIPEDE
XTONG=XSOL-50
CALL TONGUE
C
C GRABHOLD
NHA=24
DO (GRAB) M=1,NF
CALL ADVFLM(1)
CALL SOLIPEDE
GRAB CALL TONGUE
C
C ZOOM
XPAN=15
NZOOM=40
NA=6
SCNEW=0.6
SCOLD=SCALE
OD=1/SCOLD
DD=(1/SCNEW-OD)/NZOOM
ZZ=0
C
DO (ZOOM) M=1,NZOOM
C
D=1/SCOLD+DD*M
SCALE=1/D
Z=ZZ
ZZ=512*(D*SCOLD-1)
Z=ZZ-Z
X=XPAN+Z
C
CALL PAN
CALL ADVFLM(1)
CALL FLEXIPEDE
CALL TONGUE
CALL SOLIPEDE
ZOOM CONTINUE
100 CONTINUE
C
NHA=24
CALL HOLD(1,NHA)
C
C OPEN
OS=3
OJ=0.673
NOPEN=52
DO (OPEN) M=1,NOPEN
CALL ADVFLM(1)
CALL OPEN(OS,OJ)
CALL FLEXIPEDE
CALL TONGUE
CALL SOLIPEDE
OPEN CONTINUE
C
NHB=24
CALL HOLD(1,NHB)
C
C PULL
DPULL=150
NPULL=3
DO(PULL) N=1,NPULL
CALL ADVFLM(1)
XTONG=XTONG-DPULL
XSOL=XTONG+50
CALL FLEXIPEDE
CALL TONGUE
CALL PULSOL(N)
PULL CONTINUE
C
C HLDIN
NHLDIN=24
XSOL=XHEAD+100
DO (HLDIN) M=1,NHLDIN
CALL ADVFLM(1)
CALL FLEXIPEDE
CALL PULSOL(4)
HLDIN CONTINUE
C
C GULP
NS=11
NA=NA+6
X=50
Z=0
CALL PAN
NGULP=24
DO (GULP) M=1,NGULP
CALL ADVFLM(1)
CALL FLEXIPEDE
GULP CONTINUE
C
C SHUT
SS=-4
SJ=-0.795
NSHUT=44
DO (SHUT) N=1,NSHUT
CALL ADVFLM(1)
CALL OPEN(SS,SJ)
CALL FLEXIPEDE
SHUT CONTINUE
C
NHC=24
CALL HOLD(2,NHC)
C
C EXIT
NEXIT=270
DO(EXIT) N=1,NEXIT
CALL ADVFLM(1)
CALL WALK
CALL FLEXIPEDE
EXIT CONTINUE
C
CALL IDEND
C
STOP
C
SUBROUTINE FLEXIPEDE
DO(FLEX) N=1,NS
CALL START (XHEAD-XBOD(N),BOT)
CALL TO (XHEAD+XK(N,NA),BOT-YK(N,NA))
CALL TO (XHEAD+XFT(N,NA),GRND+YFT(N,NA))
CALL DRAW (FOOT, NFOOT, XHEAD+XFT(N,NA),GRND+YFT(N,NA))
CALL DRAW(BODY, NBODY, XHEAD-XBOD(N), BOT)
FLEX CONTINUE
C
CALL DRAW (SKULL, NSKULL, XHEAD, BOT+YSKULL)
CALL TO (XHEAD+DJAW(1,1), BOT+YJAW+DJAW(2,1))
CALL DRAW (DJAW, NJAW, XHEAD, BOT+YJAW)
CALL DRAW (EYE, NEYE, XHEAD, BOT+YSKULL)
C
RETURN
END
C
SUBROUTINE SOLIPEDE
C
CALL START(XSOL,SBOT)
CALL TO(XSOL+XKS(L),SBOT-YKS(L))
CALL TO(XSFTA,YSTFA)
CALL DRAW(FOOT,NFOOT,XSFTA,YSTFA)
CALL DRAW(SOLIBOD,NSOLIBOD,XSOL,SBOT)
RETURN
END
C
SUBROUTINE WALK
NA=NA+1
IF(NA.GT.NAM) NA=1
XHEAD=XHEAD+DX
RETURN
END
C
SUBROUTINE LEAP
L=L+1
IF(L.GT.LM) L=1
XSOL = XSOL+DXSOL
SBOT = SGRND+YSOL(L)
XSFTA = XSOL+XSFT(L)
YSFTA = SGRND+YSFT(L)
RETURN
END
C
SUBROUTINE OPEN(IS,IJ)
YSKULL=YSKULL+IS
YJAW=YJAW-IJ
RETURN
END
C
SUBROUTINE TONGUE
CALL DRAW(PAD,NPAD,XTONG,BOT)
DO 1 K=1,2
CALL START (XTONG+PAD(1,K), BOT+PAD(2,K))
1 CALL TO (XHEAD+50,BOT+PAD(2,K))
RETURN
END
C
SUBROUTINE HOLD(K,N)
DO I = 1,N
CALL ADVFLM(1)
CALL FLEXIPEDE
IF(K=1) BEGIN
CALL SOLIPEDE
CALL TONGUE
END
1 CONTINUE
RETURN
END
C
SUBROTINE PULSOL(J)
CALL DRAW (SOLIBOD,NSOLIBOD,XSOL,BOT)
CALL START (XSOL,BOT)
CALL TO (XSOL+PL(1,J), BOT-PL(2,J))
CALL DRAW (FOOT,NFOOT, XSOL+PL(3,J), BOT-PL(4,J))
RETURN
END
C
SUBROUTINE FLEXIGO
BOT=GRND+120
DO 1 I=1,NF
CALL ADVFLM(1)
CALL WALK
CALL FLEXIPEDE
1 CONTINUE
RETURN
END
C
SUBROUTINE SOLIHOP
DO 1 I=1,NF
CALL ADVFLM(1)
CALL LEAP
CALL SOLIPEDE
1 CONTINUE
RETURN
END
C
SUBROUTINE BLANK
DO 1 I=1,NF
CALL ADVFLM(1)
1 CONTINUE
RETURN
END
C
SUBROUTINE PAN
XHEAD=XHEAD+X
XSOL=XSOL+X
XTONG=XTONG+X
XSFTA=XSFTA+X
YSFTA=YSFTA+2
SGRND=SGRND+2
GRND=GRND+2
SBOT=SBOT+2
BOT=GRND+120
RETURN
END
C
SUBROUTINE START(XX,YY)
XS=INT(XX*SCALE)
YS =1023-INT(YY*SCALE)
IF(INVX.NE.0) XS=1023-XS
RETURN
END
SUBROUTINE TO(XX,YY)
XF=INT(XX*SCALE)
YF = 1023-INT(YY*SCALE)
IF(INVX.NE.0) XF=1023-XF
CALL VECTOR(XS,YS,XF,YF)
XS=XF
YS=YF
RETURN
END
SUBROUTINE DRAW(FIG,N,XORGN,YORGN)
DIMENSION FIG(2,N)
XS = INT((FIG(1,1)+XORGN)*SCALE)
YS = 1023-INT((FIG(2,1)+YORGN)*SCALE)
IF(INVX.NE.0) XS=1023-XS
DO 1 K=2,N
XF = INT((FIG(1,K)+XORGN)*SCALE)
YF = 1023-INT((FIG(2,K)+YORGN)*SCALE)
IF(INVX.NE.0) XF=1023-XF
CALL VECTOR(XS,YS,XF,YF)
XS=XF
1 YS=YF
RETURN
END
END
END
*ENTER
7/8 CARD
DATA
LEAP TRAJECTORY
80 0
120 0
192 72
248 138
288 188
312 222
320 240
312 232
288 208
248 168
192 102
120 20
7/8 CARD
DATA
WALK TABLE
48.0 -100.0 -248.0 -300.0 -352.0 -500.0 -648.0 -700.0 -752.0 -900.0-1048.0
40.0 -87.6 -246.4 -308.0 -360.0 -487.6 -646.4 -708.0 -760.0 -887.6-1046.4
32.0 -76.0 -241.6 -316.0 -368.0 -476.0 -641.6 -716.0 -768.0 -876.0-1041.6
24.0 -66.1 -233.9 -324.0 -376.0 -466.1 -633.9 -724.0 -776.0 -866.1-1033.9
16.0 -58.4 -224.0 -332.0 -384.0 -458.4 -624.0 -732.0 -784.0 -858.4-1024.0
8.0 -53.6 -212.4 -340.0 -392.0 -453.6 -612.4 -740.0 -792.0 -853.6-1012.4
0.0 -52.0 -200.0 -348.0 -400.0 -452.0 -600.0 -748.0 -800.0 -852.0-1000.0
-8.0 -60.0 -187.6 -346.4 -408.0 -460.0 -587.6 -746.4 -808.0 -860.0 -987.6
-16.0 -68.0 -176.0 -341.6 -416.0 -468.0 -576.0 -741.6 -816.0 -868.0 -976.0
-24.0 -76.0 -166.1 -333.9 -424.0 -476.0 -566.1 -733.9 -824.0 -876.0 -966.1
-32.0 -84.0 -158.4 -324.0 -432.0 -484.0 -558.4 -724.0 -832.0 -884.0 -958.4
-40.0 -92.0 -153.6 -312.4 -440.0 -492.0 -553.6 -712.4 -840.0 -892.0 -953.6
-48.0 -100.0 -152.0 -300.0 -448.0 -500.0 -552.0 -700.0 -848.0 -900.0 -952.0
-46.4 -108.0 -160.0 -287.6 -446.4 -508.0 -560.0 -687.6 -846.4 -908.0 -960.0
-41.6 -116.0 -168.0 -276.0 -441.6 -516.0 -568.0 -676.0 -841.6 -916.0 -968.0
-33.9 -124.0 -176.0 -266.1 -433.9 -524.0 -576.0 -661.1 -833.9 -924.0 -976.0
-24.0 -132.0 -184.0 -258.4 -424.0 -532.0 -584.0 -658.4 -824.0 -932.0 -984.0
-12.4 -140.0 -192.0 -253.6 -412.4 -540.0 -592.0 -653.6 -812.4 -940.0 -992.0
0.0 -148.0 -200.0 -252.0 -400.0 -548.0 -600.0 -652.0 -800.0 -948.0-1000.0
12.4 -146.4 -208.0 -260.0 -387.6 -546.4 -608.0 -660.0 -787.6 -946.4-1008.0
24.0 -141.6 -216.0 -268.0 -376.0 -541.6 -616.0 -668.0 -776.0 -941.6-1016.0
33.9 -133.9 -224.0 -276.0 -366.1 -533.9 -624.0 -676.0 -766.1 -933.9-1024.0
41.6 -124.0 -232.0 -284.0 -358.4 -524.0 -632.0 -684.0 -758.4 -924.0-1032.0
46.4 -112.4 -240.0 -292.0 -353.6 -512.4 -640.0 -692.0 -753.6 -912.4-1040.0
0.0 30.0 0.0 0.0 0.0 30.0 0.0 0.0 0.0 30.0 0.0
0.0 29.0 7.8 0.0 0.0 29.0 7.8 0.0 0.0 29.0 7.8
0.0 26.0 15.0 0.0 0.0 26.0 15.0 0.0 0.0 26.0 15.0
0.0 21.2 21.2 0.0 0.0 21.2 21.2 0.0 0.0 21.2 21.2
0.0 15.0 26.0 0.0 0.0 15.0 26.0 0.0 0.0 15.0 26.0
0.0 7.8 29.0 0.0 0.0 7.8 29.0 0.0 0.0 7.8 29.0
0.0 0.0 30.0 0.0 0.0 0.0 30.0 0.0 0.0 0.0 30.0
0.0 0.0 29.0 7.8 0.0 0.0 29.0 7.8 0.0 0.0 29.0
0.0 0.0 26.0 15.0 0.0 0.0 26.0 15.0 0.0 0.0 26.0
0.0 0.0 21.2 21.2 0.0 0.0 21.2 21.2 0.0 0.0 21.2
0.0 0.0 15.0 26.0 0.0 0.0 15.0 26.0 0.0 0.0 15.0
0.0 0.0 7.8 29.0 0.0 0.0 7.8 29.0 0.0 0.0 7.8
0.0 0.0 0.0 30.0 0.0 0.0 0.0 30.0 0.0 0.0 0.0
7.8 0.0 0.0 29.0 7.8 0.0 0.0 29.0 7.8 0.0 0.0
15.0 0.0 0.0 26.0 15.0 0.0 0.0 26.0 15.0 0.0 0.0
21.2 0.0 0.0 21.2 21.2 0.0 0.0 21.2 21.2 0.0 0.0
26.0 0.0 0.0 15.0 26.0 0.0 0.0 15.0 26.0 0.0 0.0
29.0 0.0 0.0 7.8 29.0 0.0 0.0 7.8 29.0 0.0 0.0
30.0 0.0 0.0 0.0 30.0 0.0 0.0 0.0 30.0 0.0 0.0
29.0 7.8 0.0 0.0 29.0 7.8 0.0 0.0 29.0 7.8 0.0
26.0 15.0 0.0 0.0 26.0 15.0 0.0 0.0 26.0 15.0 0.0
21.2 21.2 0.0 0.0 21.2 21.2 0.0 0.0 21.2 21.2 0.0
15.0 26.0 0.0 0.0 15.0 26.0 0.0 0.0 15.0 26.0 0.0
7.8 29.0 0.0 0.0 7.8 29.0 0.0 0.0 7.8 29.0 0.0
49.0 -46.4 -199.0 -263.9 -351.0 -446.4 -599.0 -663.9 -751.0 -846.4 -999.0
48.5 -41.5 -191.0 -268.2 -351.5 -441.5 -591.0 -668.2 -751.5 -841.5 -991.0
47.2 -39.1 -182.3 -273.2 -352.8 -439.1 -582.3 -673.2 -752.8 -839.1 -982.3
45.3 -39.0 -172.9 -278.7 -354.7 -439.0 -572.9 -678.7 -754.7 -839.0 -972.9
42.8 -40.7 -163.1 -284.8 -357.2 -440.7 -563.1 -684.8 -757.2 -840.7 -963.1
39.8 -44.6 -153.9 -291.5 -360.2 -444.6 -553.9 -691.5 -760.2 -844.6 -953.9
36.1 -51.0 -146.4 -299.0 -363.9 -451.0 -546.4 -699.0 -763.9 -851.0 -946.4
31.8 -51.5 -141.5 -291.0 -368.2 -451.5 -541.5 -691.0 -768.2 -851.5 -941.5
26.8 -52.8 -139.1 -282.3 -373.2 -452.8 -539.1 -682.3 -773.2 -852.8 -939.1
21.3 -54.7 -139.0 -272.9 -378.7 -454.7 -539.0 -672.9 -778.7 -854.7 -939.0
15.2 -57.2 -140.7 -263.1 -384.8 -457.2 -540.7 -663.1 -784.8 -857.2 -940.7
8.5 -60.2 -144.6 -253.9 -391.5 -460.2 -544.6 -653.9 -791.5 -860.2 -944.6
1.0 -63.9 -151.0 -246.4 -399.0 -463.9 -551.0 -646.4 -799.0 -863.9 -951.0
9.0 -68.2 -151.5 -241.5 -391.0 -468.2 -551.5 -641.5 -791.0 -868.2 -951.5
17.7 -73.2 -152.8 -239.1 -382.3 -473.2 -552.8 -639.1 -782.3 -873.2 -952.8
27.1 -78.7 -154.7 -239.0 -372.9 -478.7 -554.7 -639.0 -772.9 -878.7 -954.7
36.9 -84.8 -157.2 -240.7 -363.1 -484.8 -557.2 -640.7 -763.1 -884.8 -957.2
46.1 -91.5 -160.2 -244.6 -353.9 -491.5 -560.2 -644.6 -753.9 -891.5 -960.2
53.6 -99.0 -163.9 -251.0 -346.4 -499.0 -563.9 -651.0 -746.4 -899.0 -963.9
58.5 -91.0 -168.2 -251.5 -341.5 -491.0 -568.2 -651.5 -741.5 -891.0 -968.2
60.9 -82.3 -173.2 -252.8 -339.1 -482.3 -573.2 -652.8 -739.1 -882.3 -973.2
61.0 -72.9 -178.7 -254.7 -339.0 -472.9 -578.7 -654.7 -739.0 -872.9 -978.7
59.3 -63.1 -184.8 -257.2 -340.7 -463.1 -584.8 -657.2 -740.7 -863.1 -984.8
55.4 -53.9 -191.5 -260.2 -344.6 -453.9 -591.5 -660.2 -744.6 -853.9 -991.5
50.0 45.0 70.0 60.0 50.0 45.0 70.0 60.0 50.0 45.0 70.0
50.5 38.4 69.4 62.4 50.5 38.4 69.4 62.4 50.5 38.4 69.4
51.7 34.5 67.7 64.6 51.7 34.5 67.6 64.6 51.7 34.5 67.7
53.3 34.2 64.5 66.7 53.3 34.2 64.5 66.7 53.3 34.2 64.5
55.4 37.3 59.5 68.3 55.4 37.3 59.5 68.3 55.4 37.3 59.5
57.6 42.8 52.7 69.5 57.6 42.8 52.7 69.5 57.6 42.8 52.7
60.0 50.0 45.0 70.0 60.0 50.0 45.0 70.0 60.0 50.0 45.0
62.4 50.5 38.4 69.4 62.4 50.5 38.4 69.4 62.4 50.5 38.4
64.6 51.7 34.5 67.7 64.6 51.7 34.5 67.7 64.6 51.7 34.5
66.7 53.3 34.2 64.5 66.7 53.3 34.2 64.5 66.7 53.2 34.2
68.3 55.4 37.3 59.5 68.3 55.4 37.2 59.5 68.3 55.4 37.3
69.5 57.6 42.8 52.7 69.5 57.6 42.0 52.7 69.5 57.6 42.8
70.0 60.0 50.0 45.0 70.0 60.0 50.0 45.0 70.0 60.0 50.0
69.4 62.4 50.5 38.4 69.4 62.4 50.5 38.4 69.4 62.4 50.5
67.7 64.6 51.7 34.5 67.7 64.6 51.7 34.5 67.7 64.6 51.7
64.5 66.7 53.3 34.2 64.5 66.7 53.3 34.2 64.5 66.7 53.3
59.5 68.3 55.4 37.3 59.5 68.3 55.4 37.9 59.5 68.3 55.4
52.7 69.5 57.6 42.8 52.7 69.5 57.6 42.8 52.7 69.5 57.6
45.0 70.0 60.0 50.0 45.0 70.0 60.0 50.0 45.0 70.0 60.0
38.4 69.4 62.4 50.5 38.4 69.4 62.4 50.5 38.4 69.4 62.4
34.5 67.7 64.6 51.7 34.5 67.7 64.6 51.7 34.5 67.7 64.6
34.2 64.5 66.7 53.3 34.2 64.5 66.7 53.3 34.2 64.5 66.7
37.3 59.5 68.3 55.4 37.3 59.5 68.3 55.4 37.3 59.5 68.3
42.8 52.7 69.5 57.6 42.8 52.7 69.5 57.6 42.8 52.7 69.5
0.0 100.0 200.0 300.0 400.0 500.0 600.0 700.0 800.0 900.0 1000.0
Four subroutines were not found called IDST, IDEND, ADVFLM and VECTOR.
It turned out that these were provided as BAS cards.
We decided against reconstructing the Atlas instructions from the BAS binary cards and then trying to work out what the original
Fortran code was.
Later, Kate found in her archive confirmation that Tony had made visits to Aldermaston, Culham and Chilton to see if he could get access to the Culham BL120 or the Aldermaston SC4020 and was offered access to the BL120. Paul Nelson at Chilton offered him a Hartran Fortran version of the basic SC4020 SCORS code for generating IBM-compatible magnetic tapes for either the BL120 or the SC4020. As these were written for Hartran's Fortran compiler, Tony used these as the basis of a rewrite in London's Fortran V. The result was the BAS subroutines IDST, IDEND, ADVFLM and VECTOR which Tony used on a number of projects. To give some idea of the code, Woody Anderson did a similar recoding for the IBM 360 which he published in the UAIDE Proceedings for 1970. Tony's Fortran deck included a large set of data cards giving all the positions of the flexipede legs An earlier program must have pre-calculated these to save time in short development runs.
The ultimate goal was a Scalable Vector Graphics (SVG) definition of The Flexipede using either Javascript or SVG's declarative animation that was as close to the original as possible. The ability to repeat an animation cycle via the repeatCount attribute in SVG would greatly reduced the size of the completed SVG document.
To understand the Flexipede program itself, the decision was made for David Duce to reprogram it in Java and for Bob Hopgood to focus on generating an animation that used the full power of SVG. Although the Flexipede Program is not overly long, some of the code around the algorithms used was worth reprogramming to ensure correctness.The titles at the beginning and end were not part of the Flexipede Fortran program. Tony had mentioned to Kate that he had done these using Letraset and Kate found the original Letraset artwork in the archive and was able to produce a good rendering of these.
The existing sound track needed some filtering to make it sound more like the original. Paul Hopgood obliged.
The graphics package used was unknown initially but eventually it was clear that it was a low level set of routines that just took coordinates defined on the 1023 by 1023 grid of the microfilm recorder and output vectors given the start and end positions.
The aim here was to answer the question Is it feasible that the Fortran we have was used to create The Flexipede animation? To an author whose first exposure to Fortran was through Fortran IV in the early 1970s, the code raised a few issues. Firstly, it contains DO loops with alphabetic labels, e.g.
DO (GULP) M=1,NGULP
CALL ADVFLM(1)
CALL FLEXIPEDE
GULP CONTINUE
Secondly the program structure was unusual:
BEGIN
...
STOP
SUBROUTINE FLEXIPEDE
...
RETURN
END
...
SUBROUTINE ...
...
RETURN
END
END
END
Looking at the data flow through the program, some variables were passed through subroutine arguments, other variables were clearly shared, but the program didn't use COMMON blocks to achieve sharing. It appeared that the dialect of Fortran used supported block structuring in a similar manner to Algol and PL/1. In the absence of any Fortran compiler with these features it was decided, for pragmatic reasons, to translate the program into Java where it was straightforward to match this structure. Since this work was done, a Fortran V manual from ULCC (dated May 1967) has come to light in Tony's archive. This describes these Fortran extensions so we are confident this is the Fortran dialect used.
The aim of the Java translation was then to generate a frame-based animation from output "similar" to that produced by the original program. The four subroutines not defined in the Fortran card deck but via BAS cards were:
IDST ADVFLM(N) VECTOR(XS,YS,XF,YF) IDEND
The subroutine ADVFLM was always called with argument 1. We initially guessed, correctly, that IDST and IDEND were microfilm recorder initialisation and termination routines, ADVFLM advanced the film to a new frame and VECTOR drew a vector from (XS, YS) to (XF, YF) in the 1023 by 1023 coordinate system. Rather than generate graphical output directly from the Fortran program we generated a trace file that recorded invocations of these routines and their argument values along with a lot of other tracing information that was used during debugging and to better understand how the program was working.
The trace file was then converted to Scalable Vector Graphics (SVG) for display using a simple script written in the awk scripting language. Output from IDST and IDEND was translated to startup and termination markup. Output from VECTOR was directly translated to SVG line elements:
<line x1='XS' y1='YS' x2='XF' y2='YF' />
ADVFLM calls in the trace were translated into SVG group (g) elements so that the content of each frame was wrapped in a g element. An id attribute containing the frame number was added to each g element. For example:
<g id='f8' class='frameInvis'> <line x1='-84.00' y1='511.00' x2='-73.00' y2='545.00' /> ... </g>
The style associated with the class attribute made the group invisible (frameInvis) or visible (frameVis). Initially, all groups except the first were made invisible. JavaScript code was added to control the animation. The control panel at the top of the web document is shown below.

When the Run button is pressed a JavaScript function is invoked which in turn calls another function, UpdateAnimation() at specified intervals (24 times per second). Update animation changes the value of the class attribute of the currently visible group from frameVis to frameInvis and the next group from frameInvis to frameVis, thereby cycling through all the frames in turn. When the maximum frame count is reached the animation recycles to frame 0. Pressing the Stop button halts the animation. It turned out to be very useful in understanding the code to be able to step through the animation frame by frame (button Step) and to set a starting frame for this (number input box and button Set Start Frame).
It was by stepping through the animation frame-by-frame, in conjunction with examining the program and trace output that we discovered some transcription errors in the data cards and worked out how the flexipede is lengthened when the solipod (effectively solipede) is swallowed.
The SVG animation generated in this way is an 8.3 MB document. Representing each graphical element in the animation by a separate SVG line element is very inefficient so an additional post-processing step was added to replace sets of line elements by more compact path elements. The advantage of doing this in a post processing step was that no changes were required to the original program.
The body parts are defined by the arrays BODY, SOLIBOD, FOOT, SKULL, DJAW, EYE and PAD at the beginning of the program:
The SKULL and JAW are separate so that the flexipede can open up its head to swallow the solipede. Only the first two lines of the eye are normally drawn but the full eye is drawn when the solipede passes overhead. PAD is the suction end of the flexipede's tongue.
The storyboard of the animation is quite simple where the numbers indicate the number of frames of the activity: (1) Flexipede lumbers across screen from Left to Right (420 then 24 blank), (2) Solipede bounces across from Right to Left (150 frames then 24 blank), (3) Flexipede returns from R to L, stops as solipede bounces over its head, continues off R (100, 120, 300), (4) Solipede bounces fast from R to L and starts returning L to R when it is caught by a large tongue (34, 14, 2), (5) Pause then pan and zoom showing the long tongue of the flexipede and another pause (24, 40, 24), (6) The flexipede's jaws open, hold, tongue pulls solipede in, it is then swallowed (gulp) increasing flexipede's size by one segment, jaws close, hold, (52, 24, 3, 24, 24, 44) (7) The satisfied flexipede crosses from R to L (270). The flexipede and solipede sizes change on each crossing.
Effectively the flexipede and solipede only travel from left to right at full size but two variables adjust the size and flip the coordinate in the X-direction about the centre so that right-to-left and left-to-right traversals at various sizes can be easily achieved.
Accompanying the animation is a sound track of a flexipede that needs oiling and a sprightly bouncing solipede that Tony created. Tony told Kate that he created the film's soundtrack recording the sound of a squeaky office chair, a garage hoist, a jaw harp and himself gulping using a domestic Philips reel-to-reel tape recorder belonging to the sister of his friend, Hugh 'Ras' Riddle.
(Tony went on to create the installation 'Sidebands' with Ras, which, along with The Flexipede, was exhibited at Cybernetic Serendipity, 1968.) Tony told Kate that the sound was sneakily recorded at night at Ras's workplace - a basement lab in the medical electronics research department of Bart's Hospital.
Tony: "There was no security in those days!"
Ras: "True geeks work unlimited hours!"
Ras (laughing): "He (Tony) was facing the wrong way round on it bouncing up and down ..."
Tony (laughing): "If anybody had seen it through the window they would have wondered what was going on!"
Ras: "We thought it was hilarious. We were conscious of the absurdity of it all the way through.
Absurdity was in a way part of what one lived for. This was Tony. It was what he did."
The timings for the various events defined in the program matched those in The Flexipede film except that the holds between scenes were not the same in the released film version. Our guess is that additional blank frames were inserted at some later stage, presumably to fit the soundtrack exactly to where it should be relative to the animation and titles.
The Flexipede walk is defined by a set of arrays (XK, YK, XFT, YFT, XBOD) giving the absolute positions of the 11 legs for the 24 positions of the animation cycle which are read in from data cards. Using absolute position values somewhat obscures the fact that the leg movements are in a cycle of four (the 5th segment of the flexipede has the same leg movement as the first, the 6th the same as the second and so on. Also, the 2nd leg cycle is the same as the first but displaced by 6 places, the 3rd displaced by 12 and the 4th displaced by 18. So one leg cycle provides all the information needed to create the animation of all the legs.
The path of each leg is from the top of the leg to the knee and then to the start of the foot with the same horizontal foot for each position.
The array XBOD defines the positions of the individual segments which was one of the missing cards but easily guessed and the other missing card was the final YFT positions which had to be guessed/interpolated. Using absolute position values somewhat obscures the fact that the leg movements are in a cycle of four, that is the fifth segment of the flexipede has the same leg movement as the first, the sixth the same as the second and so on. The walk, therefore, in relative coordinates, only needs the first four of the 11 entries. Also, the second leg cycle is the same as the first but displaced by 6 places, the third displaced by 12 and the fourth displaced by 18. So actually one leg cycle provides all the information needed.The walk tables define (XFT, YFT), (XK, YK) for the 24 frames in the walk cycle.
The path of each leg is basically the top of the leg at (0,GRND+120), the knee at (XK,YK) and the start of the foot at (XFT,GRND+YFT). The coordinate system had the Y axis going upwards while the microfilm recorders had it going downwards. Changing the Y to go downwards with the origin at the top of the leg gives us an SVG path of:
M0,0 l XK,YK l XFT-XK,120-YFT-YK l 0,10 l40,0 l-40,-10
M defines the position at the top of the leg, l gives the X,Y distances from the previous point. The last three l values define the foot.
So in relative coordinates, the first leg cycle before the foot is:
M0,0 l 49.0, 50.0 l -1.0, 70.0 M0,0 l 48.5, 50.5 l -8.5, 69.5 M0,0 l 47.2, 51.7 l -15.2, 68.3 M0,0 l 45.3, 53.3 l -21.3, 66.7 M0,0 l 42.8, 55.4 l -26.8, 64.0 M0,0 l 39.8, 57.6 l -31.8, 62.4 M0,0 l 36.1, 60.0 l -36.1, 60.0 M0,0 l 31.8, 62.4 l -39.8, 57.6 M0,0 l 26.8, 64.6 l -42.8, 55.4 M0,0 l 21.3, 66.7 l -45.3, 53.3 M0,0 l 15.2, 68.3 l -47.2, 51.7 M0,0 l 8.5, 69.5 l -48.5, 50.5 M0,0 l 1.0, 70.0 l -49.0, 50.0 M0,0 l 9.0, 69.4 l -55.4, 42.8 M0,0 l 17.7, 67.7 l -59.3, 37.3 M0,0 l 27.1, 64.5 l -61.0, 34.3 M0,0 l 36.9, 59.5 l -60.9, 34.5 M0,0 l 46.1, 52.7 l -58.5, 38.3 M0,0 l 53.6, 45.0 l -53.6, 45.0 M0,0 l 58.5, 38.4 l -46.1, 52.6 M0,0 l 60.9, 34.5 l -36.9, 59.5 M0,0 l 61.0, 34.2 l -27.1, 64.6 M0,0 l 59.3, 37.3 l -17.7, 67.7 M0,0 l 55.4, 42.8 l -9.0, 69.4
The second leg cycle starts:
M0,0 l 53.6, 45.0 l -53.6, 45.0 M0,0 l 58.5, 38.4 l -46.1, 52.6 M0,0 l 60.9, 34.5 l -36.9, 59.5
The third leg cycle starts:
M0,0 l 1.0, 70.0 l -49.0, 50.0 M0,0 l 9.0, 69.4 l -55.4, 42.8 M0,0 l 17.7, 67.7 l -59.3, 37.3
The fourth leg cycle starts:
M0,0 l 36.1, 60.0 l -36.1, 60.0 M0,0 l 31.8, 62.4 l -39.8, 57.6 M0,0 l 26.8, 64.6 l -42.8, 55.4
The 24 leg positions are shown below. The dashed lines are the starting positions from right to left of the animation of the first four legs which then get repeated for the following legs.
Going from right to left, the foot positions move backwards along the ground then come forward on the curve of a circle. The knee positions are calculated using a similar algorithm we believe to that which is used for the solipede.
For each traversal of the flexipede variables are set to give its size and direction of travel. For the initial walk the legs cycle through the 24 positions as the flexipede traverses the screen over 420 frames. At 24 frames per cycle that amounts to 17.5 repeats which SVG can handle so only a single 24 loop needs to be declared but with a repeatCount attribute set to 17.5.
The path of the Solipede is defined by the leap trajectory which gives the Y position of the top of leg and how far the foot is off the ground for a 12-frame rather than 24-frame cycle. Most of the y-values are defined as:
y = -72 + 112×t - ½×16×t2
This is the standard vertical positioning of an object with an initial velocity of 112 units per sec and a gravity of 16 units per sec2. The initial position being at y=-72. In the leap trajectory, all the values correspond with the formula above except for the initial positions that effectively generate the initial velocity.
There is a large constant forward movement of the solipede together with a smaller additional forward movement in the first half of the leap cycle and the same move backward in the second half that simulates the added velocity forward at the start of the cycle after the jump starts and the slowing down of the solipede during the cycle. This is similar to the trajectory of a running kangaroo.
The solipede foot moves forward 6 units each frame of the cycle and the position of the knee is calculated from the X and Y positions of the foot and the Y-position of the top of the leg defined by the leap trajectory table. This could be regarded as a straightforward four-bar linkage with the foot position and top of leg constraining the knee position by the fixed lengths of the upper and lower leg (similar to cycling).
The example below shows a similar movement on a complete flexipede.
The basic motion from the leap trajectory table is shown together with a forward movement to give the leaping motion.
The leap program is designed to give a reasonably correct positioning for the knee in this motion. This is done by a heuristic that moves the knee up and forward depending on the distance that the foot is in front of the top of the leg. The line between the top of the leg and the foot is moved forward as though the leg was longer creating a parallel line that stops at an arbitrary line above the top of the leg. The knee is then positioned half way between the original half way point and the new one. The choice of heuristic seems to be one that Tony invented. Perhaps flexipedes and solipedes do have legs that stretch and contract.
The table of positions that define the flexipede's walk appear to be defined in a similar way. An earlier program found in the deck of cards may be an early version of the program that generated the flexipede's leg movements.
The cycle of the animated solipede jump is shown below:
The solipede capture is reasonably complicated as the solipede has to be sucked into the open jaws without the legs dangling below and then to right the legs once the capture has occurred.
The array defined by:
REAL PL(4,4)/50.,50.,90.,110.,66.,25.,120.,70.,69.,10.,136.,30.,70.,0.,140.,6./
gives the intermediate coordinates of the solipede leg during capture. Once captured, the head moves forward half a body segment length and the body back by the same amount thus creating a flexipede with an extra segment that walks off satisfied.
One unusal aspect of the Flexipede film was that on reaching the edge of the screen area it starts to generate a wall. Effectively the lines of the Flexipede that are greater than 1023 in the X direction or less than zero have the X-coordinate changed to either 1023 or zero thus creating a set of vertical lines. With the microfilm recorder overstriking the lines in question giving a much more intense (thicker line) that appears on the film image.
That confirmed that the library used to draw the Flexipede was relatively low level and had not included genuine clipping at the screen boundary that was limited to lines drawn between 0 and 1023 in the X and Y directions.
The basic SCORS library on the SC4020 which Tony used to define his version of VECTOR had a routine:
CALL VECTOR(X1, Y1, X2, Y2)
The X and Y positions should be in the range 0 to 1023. As both the SC4020 and BL120 microfilm recorders only draw vectors with less than 64 increments in the X and Y direction, the VECTOR routine breaks the line into a set of segments. However, before breaking the line into sections, the SCORS VECTOR code is:
DO 400 I=1,4
IF(J(I).LT.0) J(I)=0
IF(J(I).GT.1023) J(I)=1023
400 CONTINUE
It just reduces the coordinate values to the relevant boundary value and this gives the exact effect seen on the Flexipede film.
This pretty well confirmed that Tony used the low-level SCORS routine clipping for generating the Flexipede BL120 output.
The algorithm is quite crude biting off 64-bit sections of the line to be output and finishing with whatever is left in the final section.
An animation of The Flexipede shows the SCORS clip as the flexipede emeges from a wall on the left and exits via one on the right.
The only way to be absolutely sure would of course be to work out what the 38 binary BAS cards for VECTOR actually did. That would entail examining over 500 Atlas machine instructions that the Fortran compiler generated for the subroutine VECTOR. However, the code for changing the coordinates outside the plotting area needs to be done almost immediately so the code would be close to the top of the subroutine.
VECTOR00, the first card indicated that the total length of the routine in octal was 1030(8) and that the compilation took place on the 27 June 1966 so the routine had been in use for quite some time.

BAS cards are relatively easy to read but quite time consuming. Columns 7 and 8 give the relocatable address for the 16 instructions on the card. On loading, addresses will be incremented to the actual position in the memory where the routine will be executed. Starting at column 9 the columns 9-12 have the 48 hole positions making up the first 48-bit Atlas word. A hole punched indicates a 1 and no hole punched a zero. You start at the top of the first column and finish at the bottom of the fourth column. Columns 13-16 give the next word and so on. What you find may be an Atlas instruction, alternatively it can be a data value. Unless you know what the code generated by the compiler is likely to be, it is a bit hit and miss trying to work out which it is. It is somewhat helped by the columns 2-4 that say whether each half-word on the card contains an address that needs to be relocated.
After decoding the first few BAS cards it appeared that both INTEGER and REAL variables were using floating point arithmetic to do calculations and that the integer operations were using the unstandardised floating point arithmetic which kept the integer values in the lower right-hand bits of the 48-bit word. Also the first few cards seemed to be taking the subroutine parameters and storing them in consecutive positions in the relocatable storage which is what you would expect if the plan was to do some tests in a DO loop for values greater than 1023 or less than zero.
Things got more interesting around cards VECTOR05 and VECTOR06.

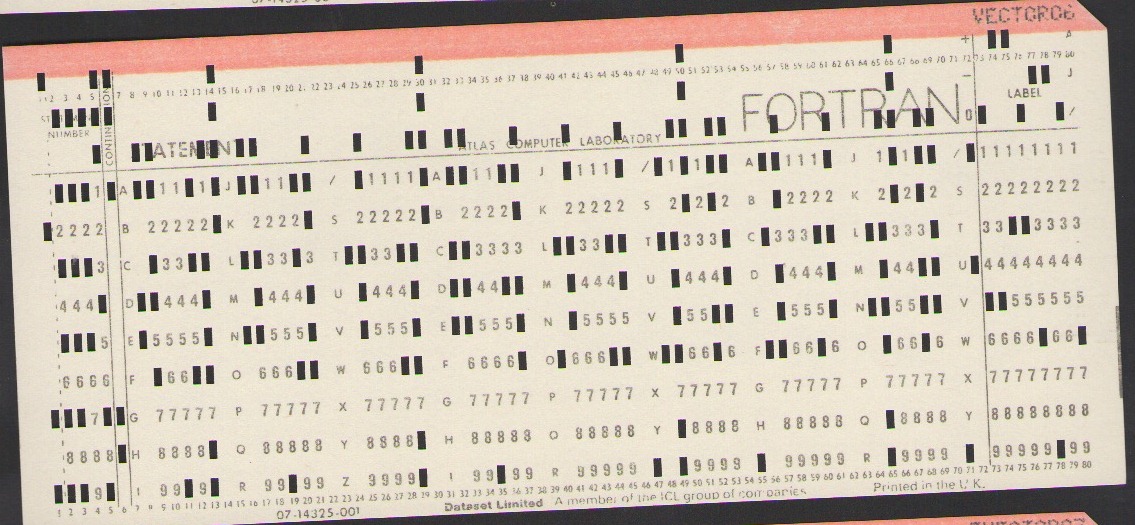
VECTOR05 is defining the contents of locations 126(8) to 145(8) and VECTOR06 from 146(8) to 165(8).
Starting at column 53 on VECTOR05 are the instructions in positions 141(8) to 145(8) and starting at column 9 on VECTOR06 are the instructions in positions 146(8) onwards.
53-56 0011011100 0000000 0000000 000000000000 000001000000 141 57-60 0010011110 1111111 0000000 000000000000 001100101000 142 61-64 0011011100 0000000 0000000 000000000001 000100100000 143 65-68 0011011100 0000000 0000000 000000000000 000001000000 144 69-72 0011011100 0000000 0000000 000000000000 000001000000 145 9-12 0011011010 0000000 0000000 000000000001 000101001000 146 13-16 0010011110 1111111 0000000 000000000000 001101010000 147 17-20 0011011100 0000000 0000000 000000000001 000101001000 150 21-24 0011101110 0000000 0000000 000000000000 000001000000 151
The first 10 bits give the instruction, the next 7 bits the first B-register called Ba, the next 7 bits the second B-register called Bm and the remaining 24 bits give the address. The top bit of the instruction indicates an extracode which doesn't get used here. The next 9 bits give the octal value of the instruction. Using the standard Atlas layout for machine instructions (the B-registers are in decimal) gives:
141 0334 0 0 10 Load storage location 10 into the floating point accumulator (Acc) 142 0236 127 0 145 Jump to address 145 if Acc is greater or equal to zero 143 0334 0 0 1044 Otherwise load the contents of address 1044 into Acc 144 0334 0 0 10 Store the contents of Acc in to address 10 145 0334 0 0 10 Store the contents of Acc in to address 10 146 0332 0 0 1051 Negate Acc and add the contents of 1051 147 0236 127 0 152 Jump to address 152 if Acc is greater or equal to zero 150 0334 0 0 1051 Otherwise load the contents of address 1051 into Acc 151 0356 0 0 10 Store contents of Acc in to address 10
So what are the contents of address 1044(8) and 1051(8)?
The answer is that we have to look at the VECTOR33 card columns 65 to 68 and columns 21 to 24 of VECTOR34.
1044 000011000000 000000000000 000000000000 000000000000 1051 000011000000 000000000000 000000000001 111111111000
Both 1044 and 1051 have an exponent of 24 which moves the fractional values leftwards to having the integer values 0 and 1023 as expected. In consequence, the sequence above is equivalent to the Fortran statements:
IF(V.LT.0) V=0
IF(V.GT.1023) V=1023
So the VECTOR subroutine does constrain values provided as parameters to be in the range 0 to 1023.
The compiled code is reasonably efficient but not optimal.
The big question was whether the card deck we found was the program that generated the film called The Flexipede. The Java program indicated that the program generated 1784 frames of film. Kate managed to find a Job Control card saying it was the final run and the lineprinter output giving the results of the run on the London Atlas. This was:
LRF91PB1, A PRITCHETT BL120 TEST
DATE 07.10.67
TIME 14.35.27
SERIAL NUMBER 12337285
REQUESTED USED COMPILE
INSTRUCTION INTERRUPTS 96000 43353 1360
COMPILE STORE 120 89
EXECUTION STORE 50 34
DECKS BLOCKS WAITING
MAGNETIC TAPES 1 37 56
IBM MAGNETIC TAPES 1 1799
STORE TIME DRUM TIME DECK TIME
16718 10 322
COMPILER NUMBER 34
F FACTOR 18
BC 1 758
BC 2 762
INPUT 0 11 BLOCKS READER 1
INPUT 1 1 BLOCKS READER 1
INPUT 2 3 BLOCKS READER 1
OUTPUT 0 648 RECORDS LINE PRINTER
OUTPUT 13 32 RECORDS ANY
The run was made on 7 October 1967, ran for 4 minutes and 31 seconds (of which 8.5 secs were for compilation). The main output was 1799 blocks of IBM magnetic tape. Magnetic tape blocks destined for the SC4020 and BL120 had a maximum of 512 instructions. New frames took place each advance film. Looking at the amount of instructions required for each flexipede frame this was well within the 512 instruction limit for all but the most complex scene. The tongue is the main drawing that needs vectors greater than 64 units long. Tapes destined for the BL120 had header and footer frames added to identify whose output it was. In consequence, the flexipede program generating 1784 film frames would require a few more than 1784 blocks of IBM tape so 1799 blocks produced is pretty well exactly what you would expect for a complete run of the Flexipede card deck. The evidence is not conclusive but leads us to believe that Kate does have the card deck that generated the film The Flexipede.
Some of the manuals that Tony had related to his use of the Culham BL120 microfilm recorder from the London Atlas are available at the Chilton website. Links to these and the various animations of The Flexipede described above are:
We would like to thank Paul Hopgood for getting rid of the worst of the background noise on the soundtrack and increasing it to a meaningful volume. Also to Victoria Marshall at Chilton who made us aware of the possibilities, provided a home for online copies of the relevant manuals etc, and gave some useful comments on the paper.