

The idea of an automatic general-purpose digital calculating machine is not a new one. It is due to Charles Babbage, who was Lucasian Professor of Mathematics in Cambridge from 1829 to 1838. Babbage was concerned with two different kinds of automatic digital calculating machine. One, which he called the difference engine, was intended for the construction of tables of functions from high-order differences, and is the better known as it was partly constructed and portions of it are still in existence. But from the point of view of recent developments Babbage's conception of the other, which he called the analytical engine, is of the greater interest. [1] [2].
This machine was to consist of three main parts; a store consisting of a number of registers, on which numbers, either data of the problem or intermediate results, could be recorded and from which they could be read; what Babbage called a mill which should be able to carry out arithmetical operations on numbers taken from the store; and a component to which Babbage did not give a name, but which we may call the controller, which should control the selection of the storage registers from which numbers were to be transferred to the mill, the arithmetical operation to be performed on them there, and the selection of the storage register to which the results were to be transferred.
The organisation planned for the analytical engine, and analysis of the organisation of a calculation done by hand methods with the assistance of a desk machine, illustrate the main functions which must be provided in an automatic digital calculating machine, namely storage (of numerical data, of tabular material, of intermediate numerical results, and of operating instructions), arithmetical operations, and control of the sequence of operations. The means of storage and control are at least as important as the means of carrying out arithmetical operations. The control system should allow the possibility, after one operation has been carried out, of selecting automatically the next instruction according to some criterion evaluated in the course of the calculation. Over 100 years ago; Babbage had recognised the importance of providing this facility, and had devised a mechanism for the purpose.
There are several different kinds of physical components and events which can be used for the representation of numbers in a machine. Many of these have two, and only two, mutually exclusive indications, which can be used to represent the digits 0 and 1; examples are a position on a paper tape, at which either a hole or no hole may be punched, an electrical relay, an electronic valve used as an on-off element, or a line which may be at one of two electrical potentials. Use of such two-indication elements suggests the use of a binary representation of numbers in the machine, but does not impose it, since it is possible in various ways to code decimal digits into a group of two-indication elements. Use of a binary representation of numbers is fashionable in the present stage of development of calculating machines, though at least two now under consideration, the Harvard Mark III of Aiken and the Univac of Eckert and Hauchly, are to work with numbers in coded decimal form.
Apart from the use of decimal or binary form, numbers can be represented in two ways, usually called parallel and serial. Suppose, for example; a number in binary form is represented by a set of indications each consisting of the presence of an electrical pulse, representing the digit 1, or the absence of a pulse representing 0. The signals representing the successive digits of a number can either be applied to a number of lines, equal to the number of digits, so as to occur simultaneously at a storage or arithmetical unit, or they can be applied in a time sequence, to a single line. The former is a parallel representation, the latter a serial representation. It is possible to have a mixed representation as in the Harvard Mark III machine, in which a coded form of each decimal digit is represented in parallel form on four lines, but successive decimal digits are treated serially. The operation of the arithmetical unit itself may be parallel, when all digits of a number are handled simultaneously, or serial when they are dealt with successively.
As an example of arithmetical operation, consider addition. This can be done in two ways; by counting, which is successive addition of units, or by the use of an addition table; with a binary representation of numbers there is no distinction between these. Addition can be carried out as a serial process, being performed successively in the successive decimal (or binary) places starting from the least significant (which should therefore come first in time, in a serial representation of numbers), or as a parallel process. In the latter case the process has two stages; in the first, the addition is made in each digital position separately, the carry-over figures being recorded but not added in; and in the second the carry-over figures are added. It might at first sight seem that the process of carry-over would have to be successive, but, as Babbage had already recognised, this is not necessary. He devised a mechanism to perform the carry-over as a parallel operation, and electrical means of doing simultaneous carry-over are used in the ENIAC and in Booth's A.R.C.
The first automatic digital computer was the Automatic Sequence-controlled Calculator (Harvard Mark I calculator), [3] [4], developed by Professor Aiken of Harvard and the I.B.M. Company and now installed in the Computation Laboratory at Harvard; this uses mechanical counters operated through electromagnetic clutches controlled by relays. In another machine built by Aiken [5] (Harvard Mark II) and in some built by the Bell Telephone Co. Laboratories, [6] relays are used for storage and for the arithmetical operations themselves as well as for control. The first machine making use of electronic circuits was the ENIAC of Eckert and Mauchly [7][8][9][10]; this was intended primarily for the step-by-step numerical integration of the equations of external ballistics, but the control system is flexible enough for it to be applied to a wide range of other calculations. A more recent machine, containing some features of the Harvard Mark I Calculator and some of the ENIAC, with others of its own, is the Selective Sequence Electronic Calculator of the I.B.M. Company.
I regard these machines as forming the first stage in the development of automatic digital calculating machines; those more recently completed or under construction are different enough to be regarded as a second stage. These are distinguished by two main features, firstly the use of a form of storage which gives a much greater storage capacity with rapid access, and secondly the use of a form of operating instructions which allows the modification of the instructions themselves as the calculation proceeds, and permits unrestricted use of the process of selecting the next instruction according to the result of evaluating some criterion in the course of the calculation. The different form of storage will make these machines smaller than those of the first stage, despite their much greater storage capacity, and they will probably be faster; and the form of the instruction should make them more flexible and easier to use.
An essential step in this second stage is the development of a reliable form of storage giving rapid access and large capacity with only a moderate amount of electronic equipment. There are three forms of storage which seem practicable for this purpose:-
A functional analysis of the operation of a machine using two-indication elements can be carried out by the use of a notation originally adapted by von Neumann from one devised by Pitt and McCulloch for the analysis of the relations between elements of the nervous system, which also consists of two-indication elements in that a single neuron has an all-or-none type of response to a stimulus. This notation [17] was developed by Turing, and is, I think, useful in representing in a general way how a machine works, though the designer and maintenance engineer will require diagrams more closely representing the physical structure of the actual hardware.
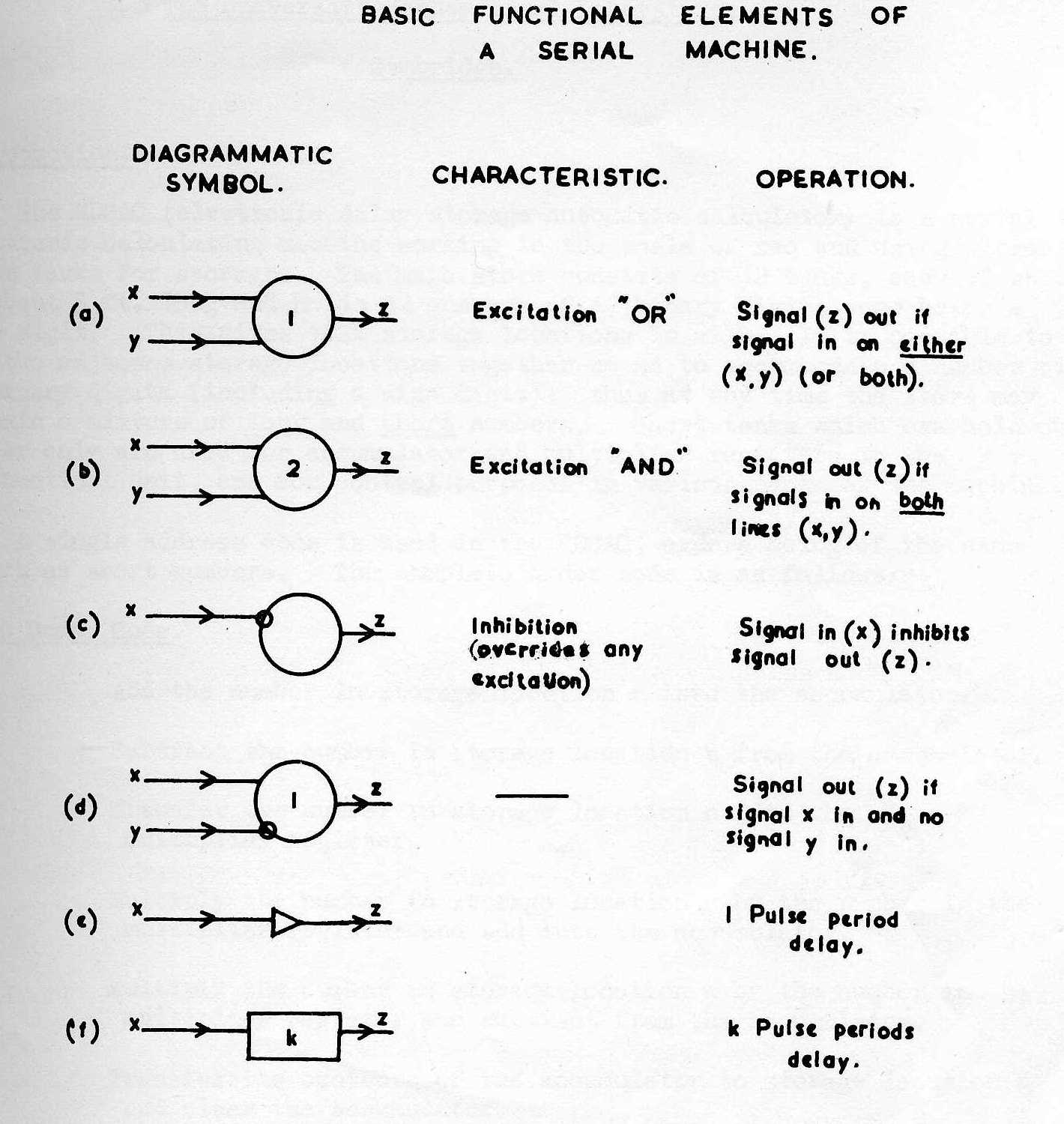
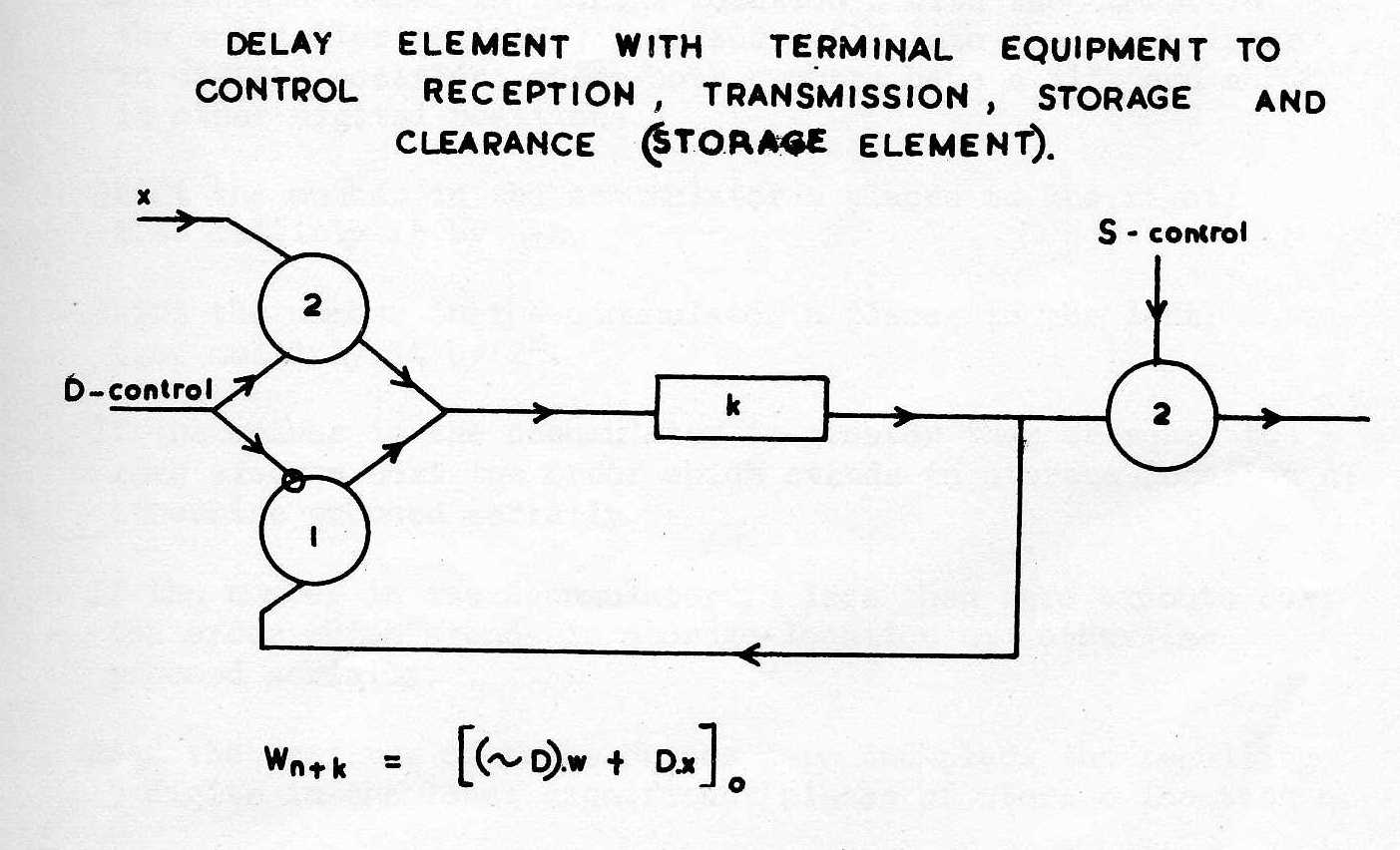
In this functional analysis, typical elements are represented by symbols shown in Fig.1. One kind, represented by a circle with one or more input lines and an output line, is an element which can be stimulated to give out a response or, perhaps, inhibited from giving one, by signals applied to its input line; the numeral in the circle (see Fig.1 a,b) represents the threshold of the element, that is the least number of simultaneous input signals required to stimulate an output; an inhibiting input is indicated as shown in Fig. 1 c.d.; these elements are regarded, ideally, as instantaneous. The other type of element is a delay element; in a serial machine, in which the pulses representing 1's recur at fixed intervals, it is convenient to measure delays in terms of this interval as units; delay elements are represented as shown in Fig.1 e.f. As an example, a storage unit formed of a delay element with terminal equipment for accepting, clearing and transmitting information is shown in Fig.2.
Regarding the use of automatic digital calculating machines, I have found that people unfamiliar with these machines have difficulty in appreciating the degree to which a calculation has to be broken down into elementary steps before such a machine can be applied to it. The basic operations of such a machine are the operations of arithmetic, possibly some logical operations (and, or, not) and the selection of the next instruction, that is all. Any calculation must be broken down into a sequence of such operations before one of these machines can be used on it. [18].
Such a process of breaking down a calculation into a sequence of elementary operations is much the same as has to be done in preparing a problem for numerical calculation by hand methods, but may have to go rather further because every step must be specified explicitly, whereas in hand calculation some steps, such as transfer of numbers between the desk machine and work sheet, are taken for granted and not stated explicitly, perhaps not consciously regarded as operations at all. But with an automatic machine a transfer has to be recognised as an operation, and coded in the sequence of operating instruction, just as definitely as an arithmetical operation.
In conclusion, I suggest some thought be given to the question of terminology [19] as it is highly likely desirable to standardise before a number of different usages become so firmly fixed as to be difficult to change.
1) C. Babbage. "Passages from the Life of a Philosopher" (Longmans, London, 1864.).
2) H.P. Babbage. "Babbages Calculating Engines" (Spon & Co. London, 1889).
3) Harvard University. Annals of the Computation Laboratory, Vol.1, (Harvard University Press, 1946).
4) Aiken, H. H. and Grace Murray Hopper, "The Automatic Sequence Controlled Calculator," Electrical Engineering, Vol. 65, 1946, pp. 384-391, 449-454, 552-528.
5) Harvard University. Annals of Comp. Lab. Vol. 16. P.69. (Harvard University Press, 1948).
6) ditto. p.41.
7) D.E. Hartree. Nature, 158. 500, 1946.
8) H.H. & A. Goldstine. "The Electronic Numerical Integrator and Computer (ENIAC)" Math. Tables and other Aids to Computation. 2. 97-110, 1946.
9) W.S. Cope and D.B. Hartree, Phil. Trans. Roy. Soc. No.827. 241 pp. 1-69 Pt.III.
10) A.W. Burks, Proc. Inst. Radio Eng. 35, 756, 1947.
11) T.K. Sharpless. Ref. (5). p.103.
12) M.V. Wilkes & W. Renwick, "An Ultrasonic Memory Unit for the EDSAC." Electronic Engineering vol 20 page 208 (1948).
13) Ref. (5), p.223.
14) F.C. Williams and T. Kilburn. Journ. Inst. Elect. Eng. 56, Pt.III No.40.
15) J. Rajchman, Ref. (5), p. 133.
16) J.W. Forrester ditto. p. 125.
17) D.R. Hartree. "Calculating Instruments and Machines" (Univ. Illinois Press 1949) Ch.8.
18) M. V. Wilkes, "Programme Design for a High Speed Automatic Calculating Machine." Journal Sci. Instr. vol 26 page 217 (1949)
19) ref. (17), p.54.