

The terms collocation and collocability were first introduced by J R Firth in his paper Modes of Meaning published in 1951. Firth does not give any explicit definition of collocation but he rather illustrates the notion by way of such examples as: 'One of the meanings of ass is its habitual collocation with an immediately preceding you silly...' Although some of his other contributions to linguistic and stylistic analysis (such as prosodic features) have had a considerable impact, his notion of collocation has not been seriously considered until the last decade. The reasons for this neglect are probably twofold: on the one hand, the rather vague terms in which he described the notion (cfr. Haskell 1970) and, on the other hand, the practical restrictions imposed by the prohibitive scale of a textual study of collocability. The latter drawback has been remedied by the introduction of the digital computer in textual analysis. As to the former, several recent attempts have been made by scholars at defining the notion collocation more precisely within the framework of modern linguistic theory. For relevant theoretical discussions on this topic, the reader is referred to the bibliography (Haas 1966, Halliday 1961, 1966, Lyons 1966, McIntosh 1966, Sinclair 1966, Van Buren 1967).
The present paper reports on a pilot study attempting to make explicit the notion of collocation in statistical and computational terms. Firth himself stressed that collocation was not to be equated with mere co-occurrence of lexical items but he always used the phrase habitual or usual collocation implying a gradation in collocability among the set of words which are found to occur in the environment of a particular item. As a technically more workable definition of collocation we borrowed the one formulated by Halliday (1961) as:
'the syntagmatic association of lexical items, quantifiable, textually, as the probability that there will occur at n removes (a distance of n lexical items) from an item x, the items a, b, c ...'
In other words, the aim is to compile a list of those syntagmatic items (collocates) significantly co-occurring with a given lexical item (node) within a specified linear distance (span). Significant collocation can be defined in statistical terms as the probability of the item x co-occurring with the items a, b, c ... being greater than might be expected from pure chance. Consider the following statistical data as being given:
Z total number of words in the text
A a given node occurring in the text Fn times
B a collocate of A occurring in the text Fc times
K number of co-occurrences of B and A
S span size, ie., the number of items on either side of the node
considered as its environment.
First must be computed the probability of B co-occurring K times with A, if B were distributed randomly in the next. Next, the difference between the expected number of co-occurrences and the observed number of co-occurrences must be evaluated. The probability of B occurring at any place where A does not occur is expressed by:
p = Fc / (Z-Fn)
The expected number of co-occurrences is given by:
E = p.Fn.S
The problem is to decide whether the difference between observed and expected frequencies is statistically significant. This can be done by means of computation of the z-score as a normal approximation to the binomial distribution (Hoel 1962) using the formula:
z = (K-E) / sqrt(Eq) (q = 1-p)
This formula has proved highly satisfactory in that it yielded a gradation among collocates which largely corresponded with our semantic intuitions. It is, however, by no means proposed as the ultimate one. Further studies on a larger scale than the present one and possibly embodying a greater variety of texts might well require modifications to it. Thus, for some nodes a Poisson distribution would be more appropriate than a binomial one. Another flaw in the formula is that it does not account for the possibility of a node co-occurring with itself within the specified span. This possibility was temporarily dismissed on account of its relative rarity. But other studies with a stylistic rather than a lexical inclination might find such aspects highly relevant. It is nevertheless hoped that the subsequent illustrations of the application of the formula will prove its relative validity. But first a few words must be said about the nature of the data.
In order to obtain a fairly comprehensive picture of the collocational relations of lexical items a very large corpus would have to be processed. Halliday (1966) quotes the figure of some 20 million running words! It is obviously not feasible even with our largest computers to process a corpus of this size. (Even the Brown University corpus of American English has a limit of 1 million words). The number of running words processed in the present pilot study amounted to 71,595. This figure is of course far off the 20 million mark but it proved sufficient for an initial methodological investigation. The data consisted of a 19th century prose work and two modern plays, namely A Christmas Carol by Charles Dickens, Each his own Wilderness by Doris Lessing and Everything in the Garden by Giles Cooper. The choice of these texts was motivated by their availability in machine readable form rather than by any stylistic considerations. Prior to the analysis a concordance and statistical information on each text (such as a frequency profile, average sentence length ...) were obtained. But the three texts were subsequently conflated as the size of each separately did not warrant results of any statistical significance. Thus, the aim of the study was not in the first place stylistic, but rather mehodological, being concerned with answering such questions as What is the optimal span size?, should grammatical items be ignored?, etc. For computational purposes, the lexical unit was defined as the graphic word ie., a sequence of characters delimited by specified word boundary markers such as space and the punctuation marks, thus adopting the same conventions used in the statistical analysis of American English at Brown University (Nelson and Kucera 1971).
The texts were processed on the Atlas computers at Manchester and Chilton. The initial stages of the program - written in Atlas Autocode - are similar to an ordinary concordance program where the context is limited to the specified span. A particular keyword being selected as node, all items occurring within the span are conflated into an alphabetical list and their number of co-occurrences with the node is counted. This list is then tested against a previously compiled dictionary consisting of an alphabetic word-frequency table for the entire text. The total number of occurrences of each collocate is subsequently recorded, after which the z-scores are computed. As initial node the item house was chosen, partly because the word count had shown it to occur with relatively high frequency (83 instances) and partly, because our intuitions about the syntagmatic bonds of this item are fairly clear, thus providing a valuable touchstone for an automatic analysis. The initial collocation set consisted of all graphic words occurring within a span of three items on either side of the node house, regardless of intervening sentence boundaries. The small size of the textual sample compelled us to discard all collocates co-occurring with house only once. This decision caused some valuable collocations to be lost (such as four-roomed house) but, conversely the inclusion of the item Amazons (occurring in the context: This house is full of Amazons ...) 'was avoided. Table 1 contains a listing, in order of absolute frequency of co-occurrence, of all items collocating at least twice with house, including indications of their total frequency in the data (Fc), their observed (K) and expected frequency of co-occurrence (E) and the respective z-scores. As might have been expected, those items co-occurring most frequently with house are grammatical. Table 2 is a re-ordering of table 1 in terms of relative collocational significance. Due to the limitations of the sample the order established is obviously not fully representative of the collocational behaviour of house in the English Language as a whole. It is, for example, highly likely that in a larger sample sold would occur more frequently in other environments than house and that Commons would stand out more clearly as forming part of the idiom House of Commons.
Where the significance limit should be drawn is in the last resort subject to the judgement of the individual investigator and to the purpose of his study. At the 0.1% level of significance statistical tables put this limit at a 2.576 z-score (Spiegel 1961). This figure was adopted as a workable hypothesis for the present study but is by no means applicable to other types of data and corpus sizes. By drawing this particular limit we run the risk of excluding from consideration unusual but creative collocations (an example of which being Dickens's use of the adjective young with house) alongside with obviously irrelevant ones. Similarly, those items with a negative z-score are excluded, although they might possibly be deemed to be of a particular stylistic interest as they seem to repel the node. However, it is our view that unusual collocation needs to be explained with reference to an explicit definition of usual collocation. The present study is an attempt to investigate how the latter can be best established.
The next question to be considered is how adequate the chosen span size was. Table 3 shows how an increase of the span size from 3 to 6 affects the sets of statistically significant collocates. All newly introduced collocates are highlighted. Some of these, such as enter, rooms, fronts, garden ... seem indeed highly relevant, whereas others such as God, Bernard, stop are to be considered intruders. An investigation at this point of the respective concordances and statistical data on each text showed that the stylistic nature of the corpus is highly relevant in defining the optimal span size. Increasing the span size resulted in effect in introducing desirable collocates from A Christmas Carol but undesirable ones from the plays. The obvious explanation lies in the marked difference between the mean sentence length which amounts to 14.03 in A Christmas Carol but only to 6.7 in the modern plays. Although by no means all significant collocates occur solely within the sentence boundaries, the majority nevertheless do. However, a general policy concerning the span size to be adopted in this pilot study could not be based upon observations of the behaviour on a single node. Other items of medium frequency were similarly tested, including verbs, adverbs and adjectives: As it proved that the majority of significant collocates do appear in the immediate vicinity of their nodes, it seemed appropriate to provisionally adopt a span of 4 for both types of data and for all nodes which were non-grammatical items, except in the case of adjectives where a span of only 2 seemed indicated.
Much more could be said at this point about further stylistic differences between the two types of data as well as about the collocational relevance of grammatical items. A case might be put forward for considering as potential collocates only those items which stand in a grammatical relation to the node. Generally speaking, this would have the effect of including only relevant items. However, unless a very sophisticated grammatical analysis which takes into account anaphoric reference is applied a great many important collocates might be lost. Consider, for example, the following quote from A Christmas Carol. It is hard to envisage at the moment a grammatical model which would be powerful enough to relate to the node face all underlined items which we felt to be lexically related to it:
Marley's face. It was not in impenetrable a shadow as the other objects in the yard were, but had a dismal light about it, like a bad lobster in a dark cellar. It was not angry or ferocious, but looked at Scrooge as Marley used to look with ghostly spectacles turned up on its ghostly forehead. The hair was curiously stirred, as if by breath or hot air; and, although the eyes were wide open, they were perfectly motionless. That, and its livid colour, made it horrible, but its horror seemed to be in spite of the face and beyond control, rather than part of its own expression.
As such a sophisticated computerised syntactic analysis is not yet available, it is hoped that the procedures proposed here will nevertheless yield some valuable results in semantic and stylistic studies of this kind.
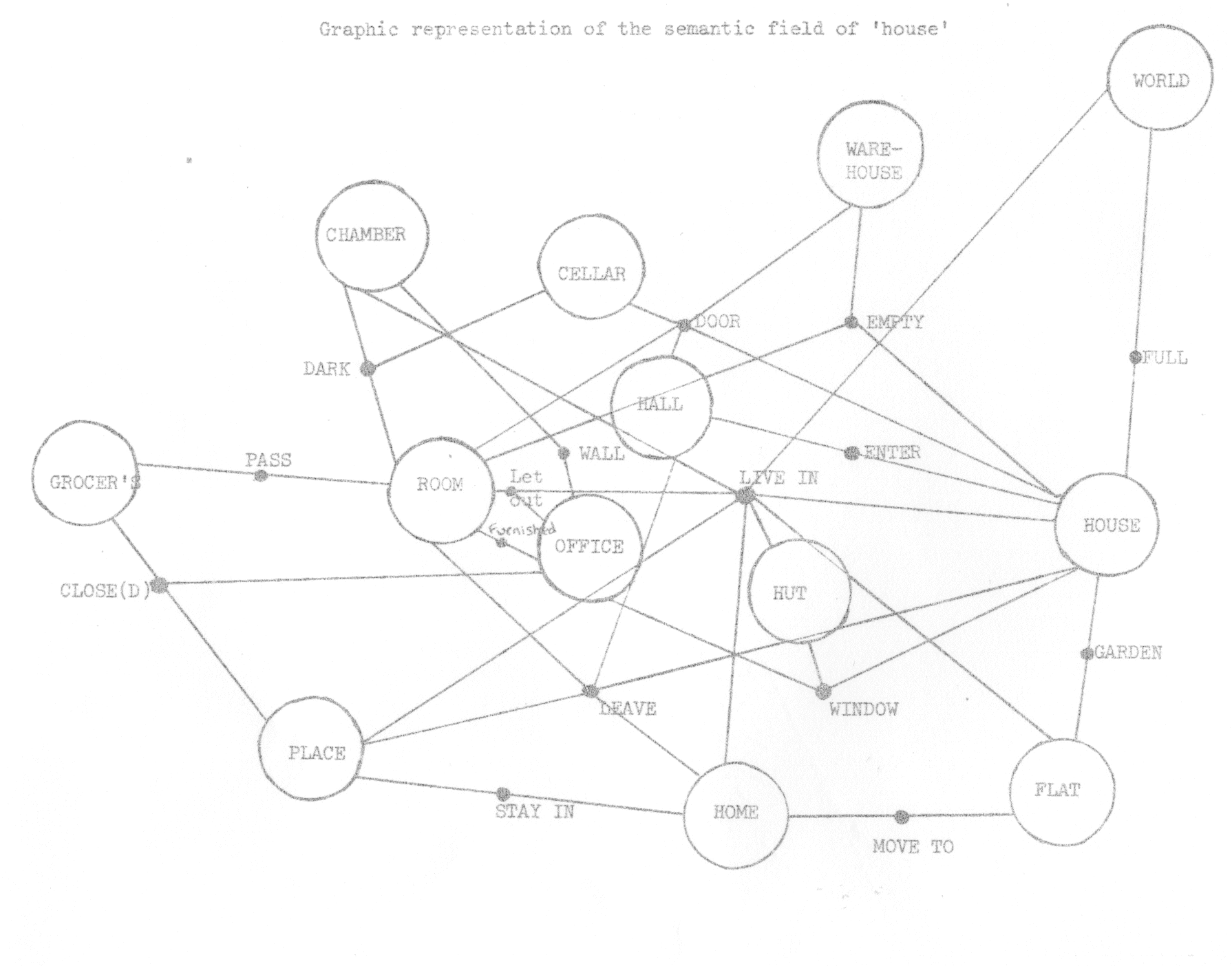
Finally, we should like to anticipate the next stage in our study of collocation. The eventual aim of a collocational analysis is not just to establish sets of syntagmatically related items but to extend these to include paradigmatically related items so that eventually a semantic field might be established. A program is being designed which will take as input the set of collocates of a given node and examine their collocational relations with other items, thus forming a network of semantically related items. Starting with the node house, a preliminary attempt was made to simulate manually such an automatic scan, hereby making use of available collocational sets and concordances. The results, which are plotted in table 4 embody a provisional semantic field of habitation terms. Considering that this field emerged from as small a sample as some 72,000 running English words it seems, apart from some obvious gaps, intuitively quite acceptable. The methods outlined in this paper when applied to a corpus of considerable size could lead to the establishment of a thesaurus of English, based on an objective and consistent analysis of how words are actually used rather than on subjective intuitions. Other stylistic applications to the analysis of the vocabulary (or even conceptual world) of an individual author are easy to envisage.
| Collocate | K | Fc | E | z-score |
|---|---|---|---|---|
| THE | 35 | 2368 | 20.6315 | 3.2278 |
| THIS | 22 | 252 | 2.1955 | 13.3937 |
| A | 15 | 1358 | 11.5661 | 0.9316 |
| OF | 13 | 1163 | 10.1327 | 0.9096 |
| I | 12 | 1674 | 14.5849 | -0.6865 |
| IN | 12 | 843 | 7.3447 | 1.7299 |
| IT | 9 | 1193 | 10.3941 | -0.4368 |
| MY | 8 | 271 | 2.3611 | 3.6780 |
| IS | 7 | 362 | 3.1539 | 2.1721 |
| HAVE | 7 | 403 | 3.5111 | 1.8682 |
| TO | 7 | 1482 | 12.9121 | -1.6660 |
| SOLD | 6 | 7 | 0.0609 | 24.0500 |
| YOU | 5 | 1711 | 14.9073 | -2.6034 |
| AND | 4 | 1568 | 13.6614 | -2.6488 |
| BUT | 4 | 383 | 3.3369 | 0.3641 |
| COMMONS | 4 | 4 | 0.0385 | 21.2416 |
| FOR | 4 | 502 | 4.3737 | -0.1794 |
| HIS | 4 | 468 | 4.0775 | -0.0385 |
| INTO | 4 | 92 | 0.8015 | 3.5792 |
| NOT | 4 | 413 | 3.5983 | 0.3221 |
| ONE | 4 | 244 | 2.1258 | 1.2879 |
| 'RE | 4 | 147 | 1.2807 | 2.5999 |
| WELL | 4 | 254 | 2.2130 | -0.1209 |
| ALL | 3 | 366 | 3.1888 | -0.1060 |
| COULD | 3 | 116 | 1.4462 | 1.9887 |
| DECORATE | 3 | 3 | 0.0261 | 19.9000 |
| EMPTY | 3 | 7- | 0.0609 | 11.9020 |
| HAS | 3 | 67 | 0.5837 | 2.9359 |
| OUT | 3 | 181 | 1.5769 | 1.1348 |
| WAS | 3 | 572 | 4.9836 | -0.0890 |
| BE | 2 | 363 | 3.1626 | -0.6557 |
| BEEN | 2 | 134 | 1.1674 | 0.7713 |
| BEFORE | 2 | 67 | 0.5837 | 1.6451 |
| LIKE | 2 | 188 | 1.6379 | 0.2833 |
| EVERY | 2 | 59 | 0.5140 | 2.0736 |
| ABOUT | 2 | 168 | 1.3522 | 0.5363 |
| BUYING | 2 | 4 | 0.0348 | 10.5270 |
| DID | 2 | 146 | 1.2729 | 0.6462 |
| DO | 2 | 374 | 3.2585 | -0.6993 |
| FAMILY | 2 | 20 | O.1742 | 4.3744 |
| FULL | 2 | 25 | 0.2178 | 3.8209 |
| GET | 2 | 101 | 0.8799 | 1.1949 |
| GHOST | 2 | 89 | 0.7754 | 1.3916 |
| IF | 2 | 268 | 2.3349 | -0.2197 |
| KNOW | 2 | 247 | 2.1520 | -0.1038 |
| LIVED | 2 | 13 | 0.1132 | 5.6067 |
| LOVES | 2 | 10 | 0.0871 | 6.4811 |
| MORE | 2 | 90 | 0.7841 | 1.3740 |
| MOTHER | 2 | 129 | 1.1239 | 0.8558 |
| MUCH | 2 | 93 | 0.8102 | 1.3227 |
| MYRA | 2 | 73 | 0.6360 | 1.7232 |
| NICE | 2 | 54 | 0.4704 | 2.3208 |
| ONLY | 2 | 60 | 0.5227 | 2.0441 |
| OTHER | 2 | 74 | 0.6447 | 1.6889 |
| OPPOSITE | 2 | 6 | 0.0522 | 8.5192 |
| OUTSIDE | 2 | 12 | 0.1045 | 5.8626 |
| PAINTING | 2 | 4 | 0.0348 | 10.5270 |
| PEOPLE | 2 | 121 | 1.0542 | 0.9220 |
| UP | 2 | 201 | 1.7512 | 1.8829 |
| REMEMBER | 2 | 26 | 0.0226 | 3.9425 |
| SEE | 2 | 127 | 1.1065 | 0.8503 |
| SOMETHING | 2 | 67 | 0.5837 | 1.9026 |
| THAT | 2 | 758 | 6.6041 | -1.8030 |
| THEY | 2 | 327 | 2.8490 | -0.5175 |
| TONY | 2 | 86 | 0.7492 | 1.4459 |
| THERE | 2 | 95 | 0.9877 | 1.2896 |
| WITH | 2 | 431 | 4.0012 | -0.9090 |
| YEARS | 2 | 50 | 0.4252 | 2.3712 |
| YES | 2 | 345 | 3.0900 | -0.5818 |
SOLD 24.0500 MORE 1.3740
COMMONS 21.2416 MUCH 1.3927
DECORATE 19.9000 WHERE 1.2896
THIS 13.3937 ONE 1.2879
EMPTY 11.9090 GET 1.1949
BUYING 10.5970 OUT 1.1348
PAINTING 10.5970 OR 0.9316
OPPOSITE 8.5192 PEOPLE 0.9440
LOVES 6.4811 OF 0.9096
OUTSIDE 5.8626 MOTHER 0.8558
LIVED 5.6067 SEE 0.8503
FAMILY 4.3744 BEEN 0.7713
REMEMBER 3.9425 DID 0.6462
FULL 3.8209 ABOUT 0.5363
MY 3.6780 BUT 0.3641
INTO 3.5792 NOT 0.3221
THE 3.2978 LIKE 0.2833
HAS 2.9359 HIS -0.0385
'RE 2.5333 WAS -0.0890
NICE 2.3908 KNOW -0.1038
YEARS 2.3712 ALL -0.1060
IS 2.1721 WELL -0.1909
EVERY 2.0736 YES -0.5818
ONLY 2.0441 WITH -0.9090
COULD 1.9807 ABOUT -0.3805
SOMETHING 1.9026 FOR -0.1794
UP 1.8829 IF -0.2197
MYRA 1.7239 IT -0.4368
OTHER 1.6889 THEY -0.5175
IN 1.7299 I -0.6865
HAVE 1.8689 BE -0.6557
BEFORE 1.6451 DO -0.6993
TONY 1.4459 TO -1.6660
GHOST 1.3916 THAT -1.8030
YOU -2.6034
AND -2.6488
Span = 3 Span = 4
collocate K Fc z-score collocate K Fc z-score
sold 6 7 24.0100 sold 6 7 20.7566
commons 4 4 21.2416 commons 4 4 18.3415
decorate 3 3 19.8000 decorate 3 3 15.8837
this 22 252 13.3337 this 22 252 10.7863
empty 3 7 11.8090 empty 3 7 10.2360
buying 2 4 10.5970 buying 2 4 9.0697
painting 2 4 10.5970 painting 2 4 9.0697
opposite 2 6 8.5192 opposite 2 6 7.5951
loves 2 10 6.4811 loves 2 10 5.5975
outside 2 12 5.8626 entered 2 10 5.5975
lived 2 13 5.6067 near 2 11 5.2373
family 2 20 4.3744 outside 2 12 4.9038
full 2 25 3.8209 lived 2 13 4.7583
remember 2 26 3.9425 remember 3 26 4.9102
my 8 271 3.6780 rooms 2 15 4.3255
into 3 92 3.5792 flat 2 18 3.8170
the 35 2368 3.2978 big 2 19 3.7878
has 2 50 2.9359 Bernard 2 20 3.6876
family 2 20 3.6676
my 9 271 3.3055
full 2 23 3.2845
into 3 92 2.8326
the 42 2368 2.3182
every 3 59 2.7971
Mrs. 2 29 2.6713
Span = 5 Span = 6
collocate K Fc z-score collocate K Fc z-score
sold 7 7 21.6383 sold 8 7 22.5581
commons 4 4 16.3571 commons 4 4 14.8871
decorate 3 3 14.1356 decorate 3 3 13.8456
fronts 2 2 11.5635 fronts 2 2 10.5971
this 22 252 9.6080 cracks 2 2 10.5971
empty 3 7 9.0914 this 22 252 8.4908
buying 2 4 8.0577 empty 3 7 8.2410
painting 2 4 8.0577 buying 2 4 7.3117
opposite 2 6 6.1350 painting 2 4 7.3117
loves 2 10 4.8677 opposite 2 6 5.8695
entered 2 10 4.8677 loves 2 10 4.3741
near 2 11 4.6050 entered 2 10 4.3741
outside 2 12 4.6050 black 2 12 3.9168
black 2 12 4.3742 near 2 11 4.1308
remember 3 26 4.2689 outside 2 12 4.1308
lived 2 13 4.1691 remember 2 26 3.7847
rooms 2 15 3.9122 lived 2 13 3.7118
garden 2 17 3.5230 rooms 2 15 3.6698
flat 2 18 3.4019 God 5 64 3.6806
big 2 19 3.2829 stop 3 27 3.2550
into 5 92 3.2795 garden 2 17 3.1308
God 4 64 3.1869 flat 2 18 3.0115
family 2 20 3.1728 every 4 59 2.9325
Bernard 2 20 3.1728 big 2 19 2.9009
my 9 271 2.8011 my 11 271 2.8854
full 2 25 2.7980 into 5 92 2.8849
family 2 20 2.7310
Bernard 2 20 2.7310
whole 2 23 2.6771
house room office home place flat hall chamber hut cellar warehouse grocer's world
live in/at * * * * * * * *
leave * * * * *
door * * * * *
empty * * *
window * * *
close * * *
dark * * *
garden * *
move * *
let out * *
furnished * *
stay in/at * *
wall * *
pass * *
enter * *
full * *
Cooper, Giles (1963) Everything in the Garden New English Dramatists - 7, pp 141-221. London: Penguin
Dickens, Charles (1922) A Christmas Carol. London: Macmillan
Firth, J.R. Modes of Meaning. Papers in Linguistics 1934-51, (1957) pp. 190-215. Oxford University Press.
Firth, J.R. (1968) A Synopsis of Linguistic Theory 1930-55. Selected Papers of J.R. Firth 1952-59 (ed. Palmer, F.R.) London: Longman.
Haas, W. (1966) Linguistic Relevance. In Memory of J.R. Firth, pp. 116-148 (ed. Bazell, C.E. et al) London: Longman
Halliday, M.A.K. (1961) Categories of the Theory of Grammar. Word, 17, 241-92
Halliday, M.A.K. (1966) Lexis as a Linguistic Level. In Memory of J.R. Firth, pp.148-63 (ed. Bazell, C.E. et al) London: Longman
Haskel, Peggy (1971) Collocations as a Measure of Stylistic Variety. The Computer in Literary and Linguistic Research, pp 159-169. (ed. Wisbey, R.A.) Cambridge University Press
Hoel, P.G. (1962) Introduction to Mathematical Statistics New York: Wiley.
Kucera, H. and Francis, W.N. (1967) Computational Analysis of present-day American English. Brown University Press.
Lessing, Dorris (1959) Each His Own Wilderness. New English Dramatists-1, pp. 11-97. London: Penguin
Lyons, John (1966) Firth's Theory of Meaning. In Memory of J.R. Firth, pp. 288-302 (ed. Bazell, C.E. et al) London: Longman
Mc Intosh, Angus (1966 ) Patterns and Ranges. Papers in General, Descri~tive and Applied Linguistics, pp. 183-199. London: Longman
Sinclair, J. McH, (1966) Beginning the Study of Lexis. In Memory of J.R. Firth, pp. 410-31 (ed. Bazell, C.E. et al) London: Longman
Spiegal, M.H. (1961) Theory and Problems of Statistics London: Schaum
Van Buren, P. (1967) Preliminary Aspects of Mechanisation in Lexis. Cahiers de Lexicology, It, 89-112, 12 71-84.