Chemical Reactions

Peter Groves and Bob Hopgood

July 1973

Some Aspects of the Production of Computer Generated Movies for Chemistry Teaching

Proceedings of the International Conference on Computers in Chemical Research and Education

Peter Groves was from the Department of Chemistry, University of Aston, Birmingham

In order to investigate some of the problems involved in the production of computer generated movies, a film on First Order Reactions has been made. This is described and some conclusions drawn regarding the feasibility of such productions by the chemistry teacher.

INTRODUCTION

Film and other visual media are today finding increasing application in many fields of education[1] [2].

They can, in a sense, add an additional dimension to teaching; for example, by introducing a greater sense of reality through the use of films of actual situations in the real world or, by means of skillful animation, illustrating abstract concepts or the postulated behaviour of microscopically invisible particles such as molecules, atoms and sub-atomic units. The visual media can also be used as aids to the presentation of information, adding clarity and, precision to a lecture or demonstration in a way that is often otherwise difficult or impossible to achieve.

Although in some disciplines film has long been recognised as a valuable instructional medium, its use in the teaching of Chemistry has been less significant. This, as some recent conferences have shown [3] [4], is not due to unawareness on the part of chemists of the potentialities of the medium. Rather it is because, in many ways, a highly structured, theoretically based subject such as chemistry presents many difficulties in the adequate and effective visual illustration of many of its aspects. Certainly film - and also television - can be used very effectively in the demonstration of experimental techniques and can help the student to acquire effective working methods. In more theoretical areas of the subject however, many difficulties can arise, these being principally related to technical production problems. Where suitable animation facilities are available - and this effectively means where adequate funds are forthcoming - important concepts can be illustrated in an informative and stimulating fashion as shown by the many excellent animated sequences in the CHEMstudy films [5]. Where budgets are more modest however these are out of the question, certainly for the teacher who wishes to make a film for his own use and not for widespread circulation and sale.

However, the advent of computers which are able to output directly to 16mm or 35mm film raises the possibility of the Chemistry teacher being able to produce his own animated movies. All that is required basically is that he should have:

1. a sufficient understanding of computer programming
2. access to a suitable computer
3. sufficient funds to pay for the computer time
4. some understanding of film production techniques - sufficient that is to permit the writing of a shooting script from which the computer program is to be derived

In order to investigate some of the problems of computer movie production one of us (P.D.G) decided to make a movie on a chemical topic. In this case factors (ii) and (iii) above presented no problems since, in the United Kingdom, universities have free access, for approved projects, to the computing facilities available at the Atlas Computer Laboratory. It was decided to make the film on some aspects of the kinetics of first order reactions since it was considered that this, being mathematically and conceptually fairly straightforward, would not present too many programming difficulties and would also be of considerable use in teaching at first year undergraduate level.

THE COMPLETED FILM

The film entitled First Order Reactions runs for six minutes and falls in to two sections. In the first section several animated graphs for the reaction sequences:

    k 
 A  ->  B
and
    k1     k2
 A  ->  B  ->  C

are displayed. The curve showing the variation with time of the concentration of reactant A, for varying values of the rate constant k, is shown dynamically. This is then repeated to show, in addition, the variation with time of the concentration of product B. A third sequence shows the variation with time of the concentrations of reactant (A), intermediate (B) and product (C) (fig. 1).

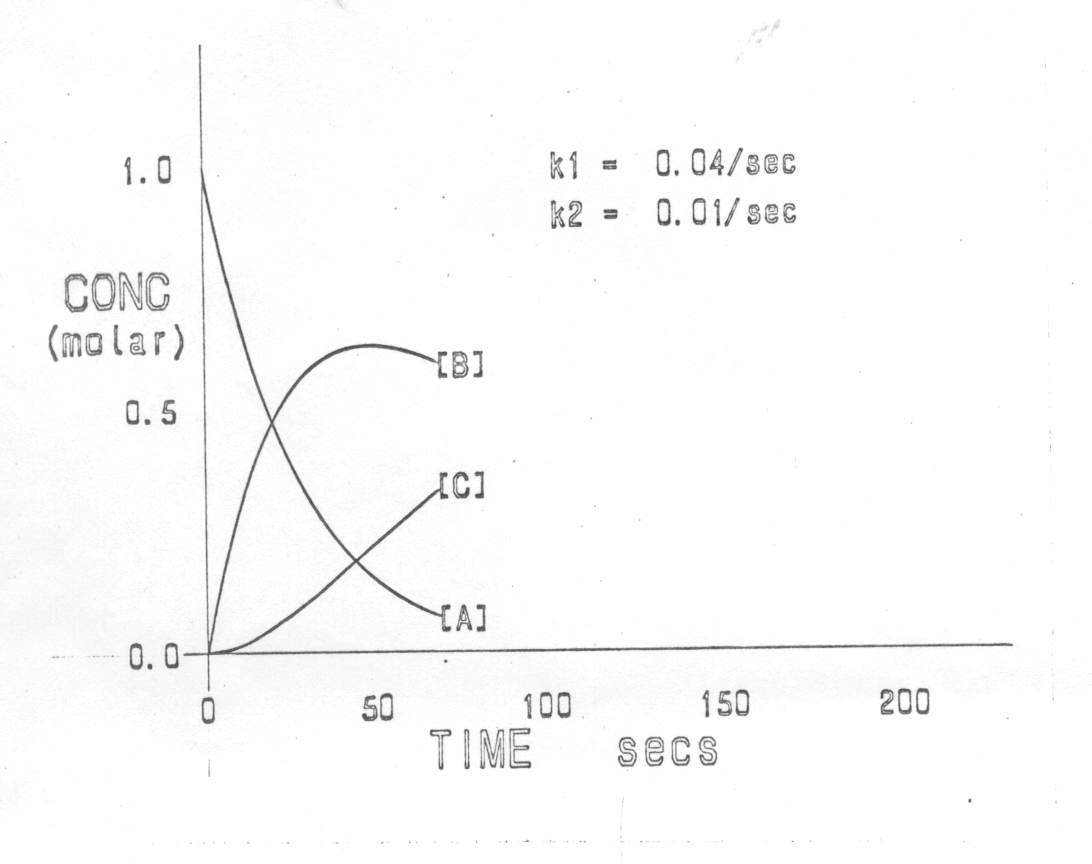
The important teaching points that can be made in this section are:

1. the rate of disappearance of reactant (and the rate of appearance of product) is initially fast but decreases with time. The growth of the curve in real time illustrates this more effectively than can a static diagram.
2. the shapes of the curves depend on the values of the rate constants. In the reaction A -> B, the point at which the curves cross (the half life) is clearly seen to decrease as the rate constant increases. In the reaction A -> B -> C the position and magnitude of [B]_max clearly decreases as, with constant k₁, the value of k₂ is increased. In the case of large values of k₂ the value of [B]_max becomes negligible. These points are most valuable in the discussion of reaction mechanisms.

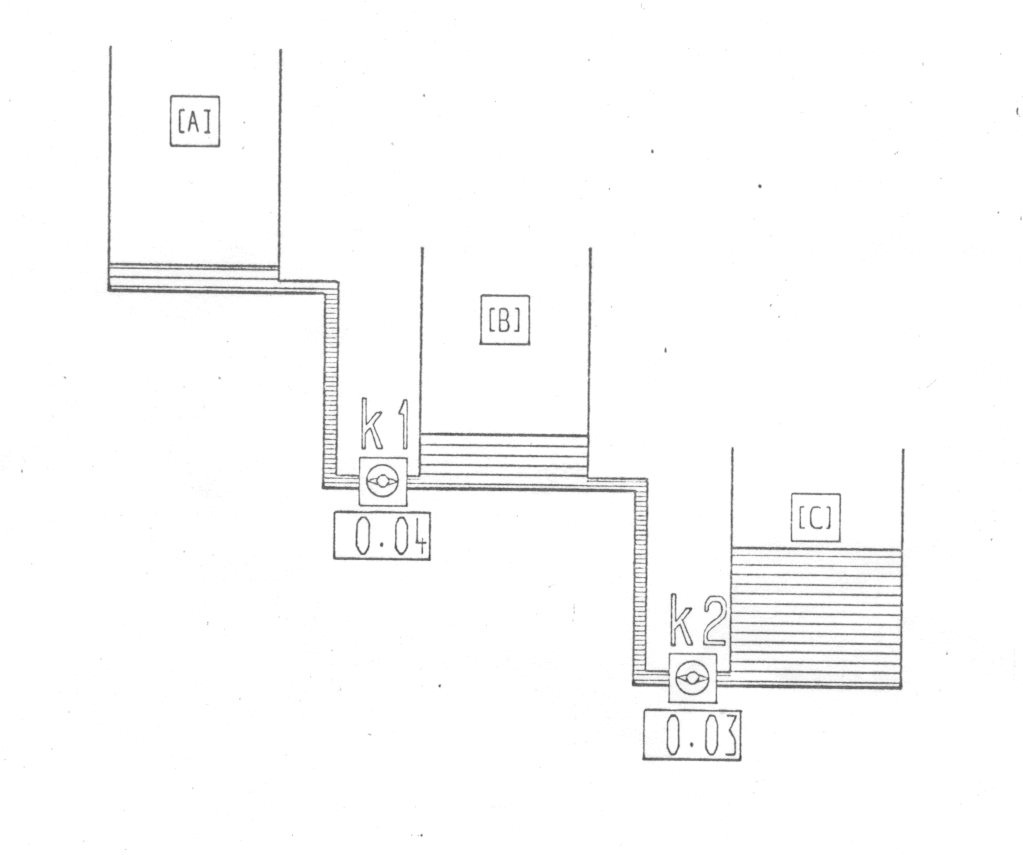
In the second section of the film, these points are further illustrated and emphasised by means of an animated diagram showing three tanks connected through pipes and taps. The first tank is filled with water which then runs out into the second tank, the rate depending on the setting of the tap (analogous to the rate constant). A second sequence, with both taps open, shows water running into the second tank and then out of this into the third tank (fig. 2).

The program was written in Algol 60 using the set of graphics procedures known as GROATS [6] and was run at the Atlas Computer Laboratory using the Chilton Atlas computer and the Stromberg Datagraphics SD4020 microfilm recorder. Running time on Atlas was 3 hours 40 minutes generating 7 million orders for the SD4020. The film stock was 16 mm. Dacomatic and this was treated as the film negative, subsequent colour prints being made on Ektachrome so resulting in a white picture on a blue background. This is aesthetically more pleasing and has a more professional appearance than the original obtained from the SD4020.

A breakdown of costs leads to the following figures:

Computing time            £750 
SD4020 time               £150
Processing and printing   £ 50
TOTAL                     £950

This does not include a charge for the author's scripting, programming and debugging time since, in the case of a film not intended for commercial distribution, these might be legitimately treated as arising out of normal university teaching/research duties. However, in a separate study, 7 minutes of quite simple animation were produced for the Open University's Foundation Course in Mathematics at a total cost of about £70 per minute of film. From the storyboard to finished film the time taken was two weeks. A more ambitious set of films for the Nuffield Foundation [7], which went through several major changes during the production, cost well over £1000 per minute of film.

CONCLUSIONS

From this work some conclusions can be drawn.

1. Useful teaching films can be made by the chemistry teacher without access to any conventional film making and animation facilities. A modest competence in Algol or Fortran is required together with some understanding of film techniques.
2. A high degree of accuracy in the representation of mathematical relationships can be achieved which can be much superior to that normally possible using conventional animation techniques.
3. Careful attention to layout and design and the use of colour printing enables a reasonably professional effect to be achieved.
4. The costs of production are currently high. This is to a large extent due to the obsolete equipment on which the film was produced. Modern microfilm recorders are capable of doing many of the operations currently being done in the main computer (for example, repetition of frames or sequences). It is likely, therefore, in the future that the computer costs will decrease significantly while the recorder costs may stay much the same. In the present film there is a fair amount of text in the form of titles, tables etc. This was all software generated, the hardware characters available from the S04020 being unsuitable for a film. A fair amount of computing time was involved in generating this text, some of which could have been deleted if costs had been more critical. Again, most of this text would have been produced using hardware characters on a modern microfilm recorder.
5. If more sophisticated effects were to be achieved then some additional facilities might be desirable. For instance the projection of three dimensional figures cannot easily be done with GROATS unless the user writes his own procedures for conversion of coordinates and for hidden line elimination. Also if colour were needed - and clearly this would be essential for some applications - access to more sophisticated hardware and/or software than is presently available at the Atlas Laboratory would be necessary. A white phosphor tube is required on the microfilm recorder together with a suitable filter switching system under program control. An alternative approach is to generate separate films in black and white for each of the colours and combine these optically using standard photographic techniques. This, however, requires accurate registration both in the microfilm recorder and in the processing laboratory. The tolerances on 16 mm. stock are such that it is virtually impossible to get a jitter-free output directly. It is necessary to produce the film initially on 35 mm. stock and reduce the final colour copy. This, of course, increases the total processing costs considerably.

FURTHER DEVELOPMENTS

Since the film was completed, additional software has been developed at the Atlas Computer Laboratory which should considerably assist in the production of chemistry films and also allow more efficient and economical program compilation. The software package is known as SPROGS [8] and allows film sequences to be defined and stored in a more flexible form. Several separately defined sequences can be made to take place at the same time on the final film, possibly interacting with each other. For example, one sequence might define the main film content with a constant camera position. A second sequence might then define camera movements and holds which depend on the events happening in the first sequence.

Further planned developments in hardware will permit users to playback and modify film sequences sitting at a visual display. Only when the animator is satisfied with the results need the actual film be generated.

ACKNOWLEDGEMENTS

The provision by the Science Research Council of computing facilities and of funds to allow the colour printing is gratefully acknowledged.

REFERENCES

1. MacKenzie N, Eraut M and Jones H.C: Teaching and Learning, An Introduction to New Methods and Resources in Higher Education, UNESCO, 1970.
2. Groves P D (Ed.): Film in Higher Education and Research, Pergamon Press, 1966.
3. British Universities Film Council: Visual Media in Chemistry, The Council, 1972.
4. Trickey D S (Ed.): Teaching and Learning in Chemistry, Sheffield Polytechnic, 1972.
5. Chemical Education Materials Study Films. University of California (distributed by Modern Learning Aids Inc, N.Y)
6. Toll D C and Hopgood F R A: GROATS Manual, Science Research Council, 1973
7. Ogborn J, Hopgood F R A and Black P J: Chance and Thermal Equilibrium, Computers in Undergraduate Science Education Proceedings, August 1970, Chicago
8. Thomas R E: SPROGS Manual, Science Research Council, 1973