

Jon Ogborn (Chelsea College, University of London) and Paul Black (Physics Department, Birmingham University) collaborated with Bob Hopgood. This was the first set of commercial films made on the SD4020 in 1968.
This paper describes a set of films made on the Stromberg DatagraphiX SD 4020 display cathode-ray-tube at the Atlas Computer Laboratory, using the GROATS package. The work has been done on behalf of the Nuffield Foundation's Science Teaching Project which is currently developing a new syllabus for teaching Advanced Level Physics to 16-18 year olds in British schools. In the course, among other things, children are introduced to a simple random game with board and counters which illustrate how chance will arrange energy among the atoms of a simplified model of a crystal. The computer films are used to show results which are hinted at by the students' own practical exercises but which are unobtainable in the classroom time available. At the present time, the course syllabus is being taught to a small number of schools in a pilot study. The films are used with a section of the course called Change and Chance which lasts for about 30 classroom periods. Its aim is to make intelligible to pupils the ideas behind the Second Law of Thermodynamics and to introduce the concept of entropy. The approach is through the statistics of molecular chaos. This has been chosen mainly because it is thought that this gives a clearer insight than other approaches but also because of the growing importance of statistical thinking in physics and other subjects. The main statistical concept introduced is that what happens in many ways will happen often. Instead of calculating what will probably happen, random games are used to show what will probably happen. It is not expected that the course will produce competent thermodynamicists. However it is hoped that pupils will be able to recognize the fundamental difference between reversible and irreversible processes. They should understand that temperature is the quantity that indicates when thermal equilibrium is reached and that heat flow is always from hot to cold. Finally they should realize that the one-way nature of heat flow can be accounted for by chance alone. It is simply what is very likely to happen.
The earlier periods in the Change and Chance section are intended to show the pupil what a one-way process is. How it is always a process involving heat exchange and is, in general, a "spreading" process. The social consequences of the Second Law are examined by looking at the consumption of fuel in the world. The idea of thermal equilibrium is introduced, and temperature is defined as a measure of thermal equilibrium.
At this point a digression is made to consider diffusion. The pupils are introduced to a simple random game of moving counters on a board. This is used to show how chance alone brings about diffusion of gases to a uniformly spread equilibrium. Molecules that can spread into a larger space will do so.
This need not be because they are pushed into the empty space but can simply be the result of chance. There are more ways of arranging the molecules when they are spread, and only rarely will chance take them back to the original unspread condition. The larger the number of molecules, the less likely is it that chance will soon produce a spontaneous reversal of diffusion. This digression will give the pupils experience of thinking about chance and about the number of ways things can happen. It also introduces them to the idea of playing random games to find out what chance will do.
The model chosen to represent heat exchanges between atoms and molecules is the Einstein solid. This consists of a regular array of harmonic oscillators, sufficiently strongly coupled to exchange energy, but not so strongly coupled as to disturb the energy levels of each oscillator. The energy levels are equally spaced and all energy exchanges are performed in multiples of a basic quantum of energy E (E = h v, where v is the oscillator frequency, h = Planck's constant). If the model is chosen to imitate a crystal with a regular array of oscillating atoms, there is the further advantage that the sites of the lattice can be numbered and counted, even though the atoms themselves are indistinguishable and cannot be labelled in principle. The quanta, of course, are not distinguishable. Boltzmann himself used a similar model, considering lumps of energy held by atoms, long before quantum ideas were discovered.
The students are then allowed to playa random game simulating the model on a board marked out into 6 x 6 = 36 squares, each square representing an atom in this hypothetical crystal. Pieces can be placed in the squares on the board to represent quanta of energy, each piece representing a quantum of energy. As each square must have an integral number of pieces, the game exhibits the properties of the Einstein solid.
A move in the game represents the exchange of one quantum of energy between two atoms. A move can be defined as follows:
A proof exists that these rules simulate the exchange of indistinguishable quanta even though the pieces are distinguishable in principle. Students may want to exchange energy only between adjacent atoms feeling that this is more realistic. This is discouraged as problems occur at board edges. It is simpler to suggest that the jumps of a quantum in the random game might be the result of several steps in a real crystal. The game is not intended to be realistic; it just behaves as a model of a crystal.
Students are given 36 pieces and are allowed to position them on the board in any order. Using a pair of dice to choose squares on the board randomly, a number of moves in the game are made. After about 20 moves, the students are asked to plot on a histogram the number of atoms with 0, 1, 2, 3 etc. quanta.
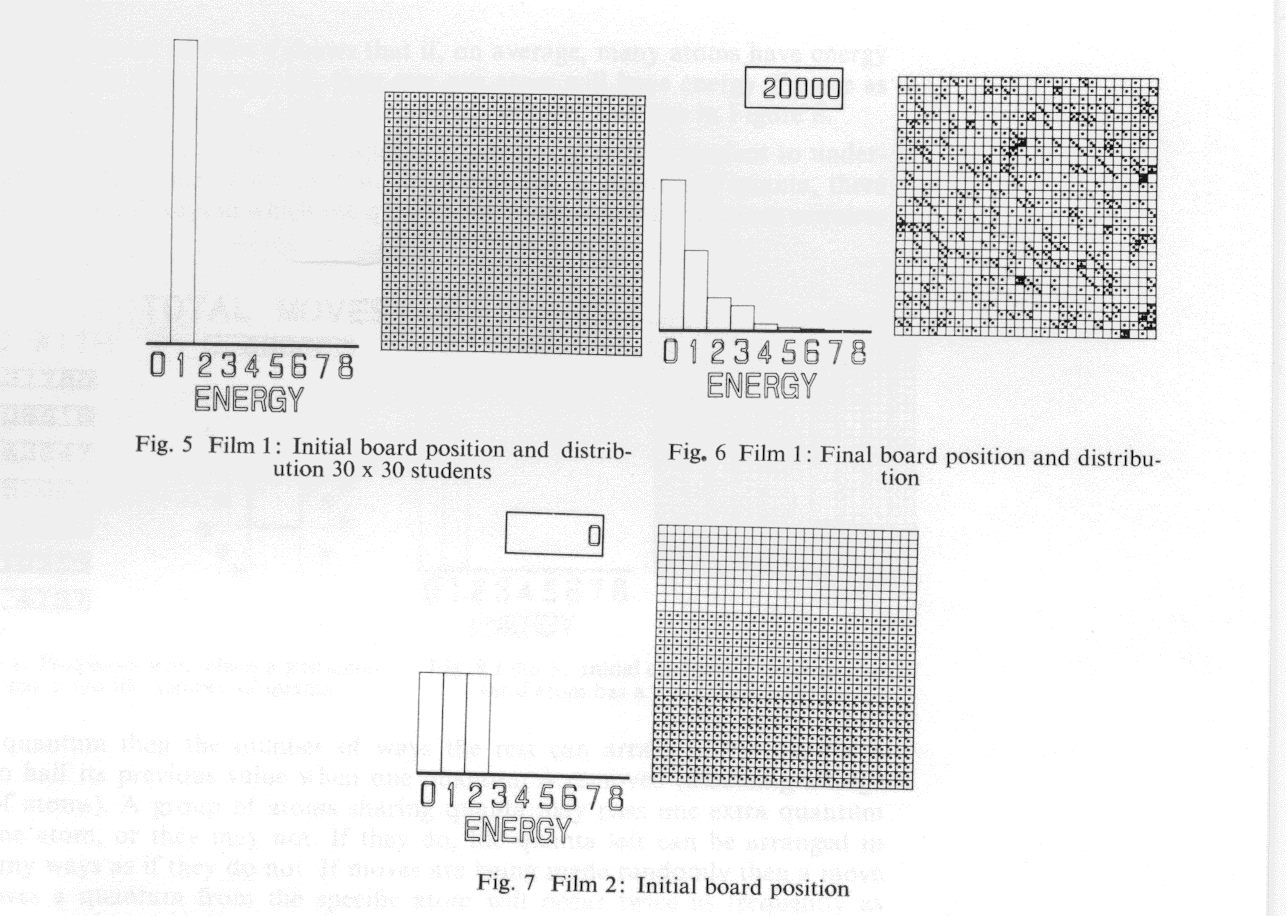
If the board is initially set with one piece on each square then the histogram initially would be like Figure 1. After 20 moves it might be like Figure 2. No recognizable pattern will have appeared over the whole class, and, if starting positions are very different, results may vary widely. The game is continued for a further 100 moves and the histograms redrawn. Now many students will have histograms that have a shape similar to Figure 3. That is, the number of atoms with no quanta of energy is larger than the number with one quanta and so on. The results around the classroom will show substantial fluctuation, and it is worthwhile taking the average of the whole class. This should have a form similar to Figure 4. It now seems likely that the ideal or average distribution will consist of a histogram where the ratio between atoms with n quanta compared with n+1 quanta is 2 for the case where the number of atoms and quanta of energy are equal [the ratio is in fact (N + q)/q for N atoms and q quanta]*. It is at this stage in the teaching that the films made on the SD4020 are introduced.
* Editor's note: This model corresponds to the classical harmonic oscillator with no zero-point energy, so that the oscillator energy in each category is
En = nhv
and the ratio of statistical weights between categories is given by the Boltzmann factor
Nn /Nn+1 = ehv/kT = R
The average energy is given by
E = hv/(R-1) = (q/N) hv
therefore R = (N + q) / q
Since the student may well be unsure that the game has progressed to a steady state and, indeed, may even be sceptical of the existence of a steady state, the computer films are introduced to resolve his doubts. They are as follows:
The computer game uses a board 30 x 30. The starting point for the first game is with one quantum of energy on each atom. The film makes the initial moves very slowly so that the student can satisfy himself that the film is playing the same game. Later the speed of playing is accelerated, and a run of 20,000 moves is played. The initial and final frames of this sequence might be as in Figures 5 and 6. Taking the average of the last 10,000 moves, it can be seen that Nn/Nn+ 1 = 2, where Nn is the number of atoms with n quanta of energy.
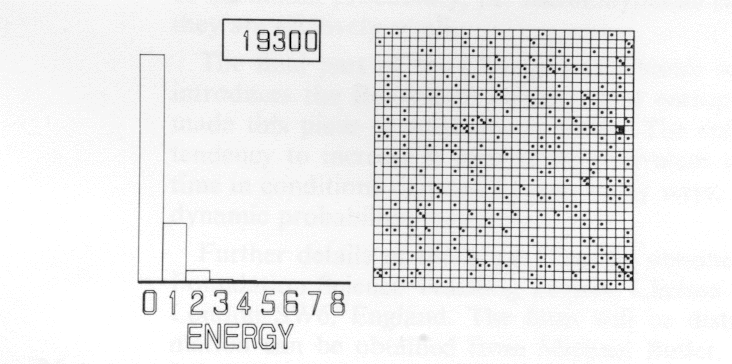
The game is repeated with 900 atoms and 900 quanta as before, but the initial board setup is changed to Figure 7. The game is replayed and the same ratio obtained.
The game is repeated with 625 atoms and 625 quanta. Again the ratio, Nn/Nn+ 1 = 2 obtained.
These three films bring out the following points:
So far, the results given above have been found as empirical facts of the computer analogue. The films are thermodynamic experiments with a computer. Whether real systems behave the same is for further experiment to show. It is important at this point to ensure that the students notice the fluctuations of the distribution at equilibrium. The equilibrium is dynamic, and if the constraints are altered (see later) the fluctuations will drive the distribution to a new equilibrium.
The game so far has suggested that many atoms have zero energy, fewer have one quantum, fewer still have two quanta. We would like to reword this as that anyone atom has no energy more often than it has one quantum and so on. In putting the results this way, a jump has been made which is not obvious. This film therefore chooses a specific square and keeps a count of how many quanta it contains over a long period. The result of Film 4 shows that if, on average, many atoms have energy E and half as many have energy 2E, then anyone atom will have energy E twice as often as it will have energy 2E. A typical frame of this film is shown in Figure 8.

This is an important result and it is equally important to get the student to understand why this takes place. If we have an equal number of atoms and quanta, there is a definite number of ways in which the quanta can be arranged. If one atom acquires an extra quantum then the number of ways the rest can arrange their quanta is reduced to half its previous value when one quantum is removed (assuming a large number of atoms). A group of atoms sharing quanta may pass one extra quantum over to one atom, or they may not. If they do, the quanta left can be arranged in half as many ways as if they do not. If moves are being made randomly then a move that removes a quantum from the specific atom will occur twice as frequently as before.
Consequently a single atom will have energy nE twice as often as it has energy (n+1)E.
It is now necessary to consider a colder model. Assuming the number of atoms is kept the same (900) then we consider a board where the number of quanta has been reduced from 900 to 300 (N atoms sharing q = N/3 quanta). Film 5 starts with the board set up as Figure 9 and runs the game until an equilibrium is reached. The ratio between the number of atoms with n quanta and (n + 1) quanta is now R = 4 (Figure 10). This ratio can be taken as a measure of temperature. The larger the ratio, the colder is the object.
Finally we wish to see what happens to our model when the hot crystal described in the first three films is allowed to interact with the cold crystal described in Film 5.
Initially the two boards with 900 and 300 quanta are allowed to achieve an equilibrium. The two boards are then brought together and moves may now take place between atoms on either board. As the film runs, quanta gradually move from the hot board to the cold board until an equal number of quanta appear on each board. The histograms for each board move from their initial distributions to the same distribution having a ratio R = 2.5 between columns (Figure 11).
The exchange of energy between these boards is a model of heat flow. The temperatures of the two boards have become equal. Heat flow from hot to cold has been demonstrated. This may look like an obvious result which does not require this amount of effort. However the important point is that this flow came about by random shuffling. Heat flow occurred spontaneously by chance. If the cold board receives an extra quantum then it now has four times as many ways of arranging quanta. Whereas the hot board only has its number of ways of arranging quanta reduced by a factor of 2. The number of ways of arranging quanta in a system is known as the thermodynamic probability of the system. If, initially, the thermodynamic probabilities of the hot and cold systems are separately WH and WC, then the combined boards have a thermodynamic probability of WH WC initially. After the movement of one quantum from hot to cold, this becomes (½WH)(4WC = 2WH WC and there are twice as many ways of distributing quanta after the flow as before. And since this configuration can occur in twice as many ways it will occur twice as often.
Flow will continue from the hot board to the cold board until the thermodynamic probability of the combined system reaches a maximum. Additional flow of energy from one board to the other in either direction results in a less likely state of the combined system, i.e., one with smaller thermodynamic probability. Hence, it is less likely to occur. As mentioned before, fluctuations can be noted about the condition of maximum probability, i.e., thermodynamic equilibrium, but for samples this large they are relatively small.
The final part of the Change and Chance section returns to the real world and introduces the Boltzmann constant and entropy. The model, it is hoped, will have made this piece of work much easier. The statement that entropy has a powerful tendency to increase is seen to be equivalent to saying that a system spends most time in conditions that can arise in many ways, i.e., in the state of maximum thermodynamic probability.
Further details of the project can be obtained from J. M. Ogborn, The Nuffield Foundation Science Teaching Project, Chelsea College, 88/90 Lillie Road, Fulham, London SW6, England. The films will be distributed commercially; further information can be obtained from Michael Butler, Penguin Education, Penguin Books Ltd., Harmondsworth, Middlesex, England.
F. R. A. Hopgood, ALGOL GROATS Manual, Atlas Computer Laboratory, Chilton, Didcot, Berks., U.K., 1969.
F. R. A. Hopgood, "GROATS, A Graphic Output System," in Proceedings of the Eighth Annual UAIDE Meeting, 1969, Users of Automatic Information Display Equipment, Coronado, California, 1970, pp. 401-410.