

Inaugural Lecture when Bob Churchhouse became Director of the Computing Centre and Professor of Computing Mathematics
You may not be aware of the fact that computers having been with us for 21 years, have now come of age (old style). Indeed Professor David Aspinall, Professor of Electrical Engineering at Swansea, recently gave his inaugural lecture on the theme The coming of age of computer technology. I shall therefore begin with a few remarks comparing the computer situation 21 years ago and today.
In 1951 there were about 15 computers in the world all of them working on essentially mathematical problems. Each machine had to be programmed in its own language for there were none of the high level programming languages which nowadays allow us to write programs in something like English and not even the concept of an operating system had been introduced. Today there are probably more than 100,000 computers in the world. At the last count, in 1965, there were over 400 high level programming languages such as FORTRAN and ALGOL, some having a variety of dialects - a proliferation surely unparalleled since the Tower of Babel- and every computer system of any size runs under the control of a sophisticated operating system.
This phenomenal development has been compared in importance with the Industrial Revolution for whereas the machines of the 19th century increased man's capacity for physical work by a factor of a few hundred, and a modern jet increases man's speed over the earth by a similar factor a computer increases man's computing and data handling capacity by a factor of more than a million.
I'll illustrate this by a simple example. At school we were taught how to solve two equations in two unknowns such as
3x - y = 1 x + y = 3 (x = 1, y = 2)
by first eliminating one of the variables. The same basic method can be used to solve 100 equations; by hand it would take us about 2 years, assuming that we worked 40 hours a week and made no mistakes. A computer such as the ICL 4-70 we have in Cardiff would solve these equations in 15 seconds. In case anyone doubts the need ever to solve 100 equations let me add that Professor Rockey and his Civil Engineers regularly turn up with 2,000 equations for solution arising from their work on bridges. It is doubtful if anyone could solve such a set by hand in a life time.
The impact of computers in areas such as engineering, crystallography, numerical analysis and so on is obvious, particularly in the Universities and Government Laboratories. Without computers much work in these areas would be impossible. In the commercial and industrial field computers are mainly used for data handling tasks such as payroll, stock control, management information systems, project scheduling and so on. Although there is nothing very surprising in such applications I do not want to give you the impression that they are uninteresting or simple for they are neither and they frequently bring substantial economic benefits. Let me quote just one example; some years ago a carpet manufacturer paid a University Programmer to apply the techniques of linear programming to the problems of manufacture of multi-coloured carpets and the computer produced a work schedule for the looms which reduced the production time by 30% thus recouping the cost of the programmer and the small amount of machine time within a few days.
Although the design of computers, programming languages and operating systems are subjects which are intrinsically worthy of study in themselves, computers would not sell commercially if they could not be applied to a wide variety of problems. Whilst certain applications were recognised from the earliest days (numerical calculations) and others (commercial data handling) soon followed, there still remain many areas where the potential of the computer has not yet been fully recognised, particularly in the Arts subjects, to a lesser extent in the economic and social sciences, and even in a few areas of pure and applied science.
This leads me to ask three questions.
The answer to the first question is that many people haven't realised the potential of computers simply because the potential has not been explained in terms that they can understand. Such people are best convinced by examples of computer usage in the area of their specialisation but this implies that at least some of their colleagues are already using computers. Thus it is first necessary to find a few imaginative pioneers.
I believe that computing is relevant to virtually every subject taught in a University and in the hope of encouraging a few pioneers and interesting everyone to some extent I want to devote most of this lecture to a description of a number of computer applications in the Arts and Sciences and elsewhere. In order to cover a wide field I shall deal very briefly with each application and then return, at the end to the unanswered questions which I posed a moment ago.
Before describing the applications I want to make one important general point: it has been my experience that two problems from widely different areas (such as archaeology and electronic engineering) have frequently proved to be fundamentally the same when prepared as programs for a computer. The same underlying features of the problem are revealed and a program applicable to one discipline may prove to be highly relevant to another. This general principle is clearly seen for example in problems which are essentially those of cluster analysis or of pattern recognition. Thus the pattern recognition problem involved in landing men at a predetermined spot on the Moon is not very different from pattern recognition problems which arise in chemistry (recognition of spectra), biology (identification of chromosomes), criminology (identification of fingerprints), or, as recently announced, the identification of diamonds.
As a first application I want to say a few words about:
That computers are essential to space research is so obvious that it hardly needs saying, but to ignore the fact would be absurd. To put men on the Moon and bring them back not only requires a network of computers on Earth but also a small computer on board the spacecraft itself. During a manned space flight NASA have five identical computers working out the orbital details simultaneously so that if one or two of the machines should fail a majority vote will still produce the right answer. Each of these computers is at least twice the power of our machine in Cardiff. The computer in the spacecraft itself carries out routine tasks during the flight and also helps the captain to identify the landing site by comparing the radar picture being received from the ground with a stored record of the radar received from the vicinity of the landing site during earlier reconnaisance flights. During the original Moon landing (Apollo XI) this radar pattern matching failed because the Moon's gravitational field was more irregular than had been realised and the spacecraft was about 3,000 yards away from its predicted position. Although the computer could have sorted the problem out, the captain of the spacecraft (Neil Armstrong) took over manual control- an action quite understandable in the circumstances. The possibility of this type of error occurring again was removed before Apollo XII was launched. The total number of programmers involved in the Moon landing programs incidentally was 1170 (70 at NASA, 700 at IBM, 400 at MIT) many of these being under thirty years of age. That a group of such a size could work as a team and complete their projects successfully on schedule is a remarkable example of project management.
From the use of computers in space let us next look at a use of computers on earth; something that affects us every day.
Expressed in mathematical terms the weather can be predicted if we can solve a set of complex non-linear partial differential equations, which treat the atmosphere as a compressible fluid with energy sources and sinks. In practice this requires a very large and powerful computer if we are to get the answers before the weather actually arrives! There is also a major problem of data acquisition: reports on the present temperature, pressure, wind speed etc., have to be received from many weather stations, ships and balloons and fed into the computer before it can begin work. The relatively small amount of information available concerning weather conditions in the Atlantic also imposes a limitation on the accuracy of the solutions. It is quite likely however that with the superior atmospheric model now being used, short term forecasts (2-3 days) will become increasingly precise. For longer term forecasting, (1-2 weeks) the problem is much more difficult but the use of satellites may help substantially here.
The Met. Office also have some very interesting research projects. They have built into their programs a model of the earth, describing all the mountain ranges, seas and land masses in great detail; also the winds, temperatures of the seas and ice caps and the heat received from the sun. With this model they can predict what would happen if someone, for example, removed the Himalayas - they simply put height(Himalayas) = 0. Let's hope nobody does this because their computer predicts that if they did Western Europe would soon be covered in ice whilst Siberia would thaw.
The usefulness of this computerised model is illustrated by another example. The winter of 1962-3 is now known to have been the most severe winter in Britain for 250 years. Was there anything unusual in the world's weather in the summer or autumn of 1962 that could account for it? The Met. Office discovered only one unusual feature: an area of the North Pacific was a few degrees warmer than usual. They therefore told their computer to warm up the appropriate area of North Pacific by the observed amount. The computer predicted that a new wind would arise which would pass north of the Canadian Rockies, near the North Pole and then over Western Europe, thus bringing masses of cold air over Britain, so producing the sort of winter that we experienced. This is an excellent example of computer simulation of a physical system allowing the experimenters to predict what would happen if the physical conditions were changed.
The long range weather forecasts issued twice a month by the Met. Office, are based upon a different idea: they compare the weather in the previous month with historic records to find the best match they can and then predict from that. This is an example of information retrieval. The retrieval of information is a problem that is as old as the human race but it has come into prominence in the last 20 years because of the enormous increase in published work and the arrival of computers.
A large number of information retrieval systems based on computers have been developed. At the more modest end of the range are the systems based upon a collection of facts, the user being limited to a series of single direct questions. For example the facts might be the prices of all the shares on the Stock Exchange for every working day during the past 2 years. The user could then ask What was the price of ICI shares on April 28th 1972? and the machine would reply 262. Such a system is easy to implement, the main problem being that of updating the data every day.
At the other end of the scale are the airline reservations systems such as BEA's BEACON and BOAC's BOADICEA. These are among the most extensive and expensive computer systems ever put together. BOADICEA, which is based upon 3 large IBM computers with several hundred terminals around the world, cost £42,000,000 to set up. The information held by the computers is a complete record on every flight including the names and addresses of all the passengers booked on the flight and the number of seats still available. The primary object of BOADICEA is to increase the load factor on the BOAC flights. The load factor is the proportion of seats occupied and quite a small increase in this ratio can make all the difference between a healthy profit and a disastrous loss for the airline. One airline, for example, says that if it could sell one more seat on every flight it would make an extra £2,000,000 each year. With BOADICEA if a booking is cancelled in say, Hong Kong, the seat can be resold within seconds in London or New York or in many other places. Since BOADICEA became operational BOAC have increased their load factor by 14%. This is an enormous increase and BOADICEA is clearly a very considerable commercial success.
In addition to seat reservations BOADICEA is used for many other tasks such as flight planning, crew scheduling, timetables and so on.
Between these two extremes there are a whole range of information retrieval systems, for example we have available in Cardiff a set of programs which enable us to find out what papers have been written on any subject in about 20 journals on computer science during the past 12 years or so. The machine provides the information in less than 30 seconds, which is quite economic. The system will work just as well on the literature of most subjects. I have little doubt that such systems will eventually become a common feature of every large library. The availability of large capacity storage devices, even in Universities, has made the outlook in this area very much brighter than most of us would have thought possible a few years ago. For example the new disc being provided at Cardiff by the Computer Board can store nearly 200 million characters of text which is enough to hold a catalogue of the titles, authors and all essential details of about a million books. On this basis several Universities could already hold a complete catalogue of the British Museum Library in their computers. Once such a catalogue has been prepared in machine readable form copies could quickly be made available for use on any sufficiently large computer anywhere in the world. Keeping the data up to date would then be relatively easy.
With bulk storage devices becoming available new areas of computer exploitation are opening up and there is considerable interest growing in the use of computers in literary research. The most fundamental tool here is the machine produced concordance and word count. A concordance program will usually produce frequency counts of the words in a text, as well as a print-out with every significant word in the text brought to the middle of the page and several words of context printed on either side. A typical page of output from a concordance of the index to a journal is shown in the first slide. The second slide shows a concordance of a few parts of the works of Shakespeare. The output from a computer is usually printed on a line printer at a speed of about 1,000 lines per minute. Whilst this is fast it does impose the limitation that only capital Roman letters with numerals, punctuation and a few extra characters are available. This is tolerable for most Western European languages but is irksome for languages such as Greek, Russian, Hebrew, and Arabic, where some form of Roman equivalents must be used, and even less satisfactory for the ancient languages involving hieroglyphics. Before I left the Atlas Laboratory I was fortunate enough to recruit as a programmer a young woman with a 1st class honours degree at Oxford in Akkadian. The Laboratory had recently acquired a device called an SC4020 which allowed us to produce cine-films, microfilms and hard copy of any graphs or pictures that we could draw. The way in which we can use the computer to produce pictures etc., is that the computer produces a set of instructions indicating that certain points on a kind of television screen are to be joined together by lines. By joining a sufficient number of selected points together, highly complex pictures can be drawn and filmed. In particular one can generate the letters of any alphabet one wishes.
The young woman (Susan Hockey) quickly mastered programming and has gone on to become expert in providing this form of output, thus making it possible for linguists to receive their output in its correct alphabetic form, complete with all diacriticials (accents, breathings, iota subscripts, etc.). Some examples of her work are shown in the next few slides which include texts in Greek, Hebrew, Arabic, Persian, Akkadian and Egyptian (see Figs. 1 and 2).


By combining her output procedures with a concordance program the way is open for literary output of the very highest quality. For the Arts people present I point out that Mrs. Hockey had no scientific training beyond O-level thus providing a counter-example to the idea that computers are only for scientists.
The use of computers in analysis of literary style is still in its infancy but there are already a number of most interesting applications. I shall briefly describe one, the work done by Alvar Ellegard [2] in deducing the identity of the author of the Junius letters - a series of anonymous political letters written to the newspapers between 1769 and 1772, all being signed Junius. The author appeared to have excellent sources of information and the letters created a sensation, being published in book form many times in Britain and abroad. Many people were suspected of being the author including Chatham, Burke, Chesterfield, Gibbon and that great wit John Wilkes, but Ellegard showed that the internal evidence based on characteristics of style clearly points to Sir Phillip Francis. The method used by Ellegard was, briefly, as follows. A word and phrase analysis was made of
From this analysis certain characteristics of Junius's style, compared to that of his contemporaries, emerged.
Thus Junius used among 35 times and never used amongst
Francis used among 66 times and used amongst twice
Other writers combined used among 521 times and used amongst 114 times.
Similarly the usage of farther compared to further turns out to be
Junius 29 - 0 Francis 42 - 15 All others 130 - 210
In most cases Junius had a preference for one form rather than another, e.g. Junius preferred oblige to force or compel, and so on.
Ellegard found over 450 such words and phrases which he could use as tests of style. The evidence from anyone such phrase may be misleading but by combining the evidence from all of them one can work out, and it is a nice exercise in applied probability theory, the odds against any particular author having been Junius. The result is overwhelming; Sir Phillip Francis comes out as 30,000-1 on favourite with everyone else heavily odds against. As an extra bonus Ellegard showed that these characteristics of Junius's style were sufficiently strong, taken together, to make it possible to test any of the unsigned texts of more than 10,000 words to see if it was written by Junius.
I regard the work of Ellegard with its combination of literary and linguistic knowledge, skilled use of computers and careful application of probability theory as a model of its kind. By such means there is a good chance of settling questions of authorship provided sufficient material is available.
There have already been two conferences on Computers in Literary and Linguistic Research, and I am happy to say that the next such conference will be held in Cardiff in April 1974.
I have already mentioned that the SC4020 output device at the Atlas Laboratory can be used for the production of cine films and one area in which such films are very valuable is education. A few years ago I was paying a social visit to a friend, Paul Black of the Physics Department at Birmingham, and he told me that he was working for a year on the Nuffield A-Level Physics project. As we talked I realised that the SC4020 might be very useful in producing educational films for this project. Paul visited the Laboratory and in collaboration with Bob Hopgood, of the Atlas Lab., produced a series of films on the subject of Chance and Thermal Equilibrium.
Each of these films is intended to be shown as part of a physics lesson; the explanation of what is going on being provided by the teacher.
In the first film we see a 30 x 30 board, each square represents an atom and each atom has one quantum or unit or energy. Thus initially there are 900 atoms each having 1 unit or energy, and no squares having zero, two, three, etc., units of energy. The computer now plays a game.
An atom is chosen at random and it loses its unit of energy which is given to another atom, also chosen at random. This completes one move in the game. We now have 898 atoms with 1 unit of energy, one atom with no energy and one atom with two units of energy.
Another move is made, an atom is chosen at random and loses a unit of energy which is given to another randomly chosen atom. At the end of this move we have 896 atoms with 1 unit of energy, two with no energy and two with two units - but there was a small chance that one of the atoms involved in the first move would also be involved in the second in which case we would now have a different result. In the film this didn't happen.
The computer now speeds up and plays 10,000 moves and we watch the counts of the number of atoms with 0, 1,2,3, etc., units of energy reaching a reasonably steady state, as predicted by the theory which the students have been taught. The computer then continues for another 10,000 moves and the Stable State is seen to persist.
There are 6 films in the set illustrating what happens if we start from a non-uniform distribution as well as other aspects of the problem. The film is an early copy and has been given to us by the Atlas Lab.
Whilst a similar film could be made by hand, as a cartoon, it would be quite impossible to show the generation of twenty thousand experiments as was done by using the computer.
More films have since been made using this equipment, for the Open University and the B.B.C.
In addition to the production of films computers also have a role to play in education in the realm of computer-aided-instruction. This is an application which has aroused some controversy. Personally I prefer to keep an open mind, believing that there are some areas where it is useful and many more where it is not.
The conventional way of getting data into a computer is via punched cards or paper tape. Similarly the conventional medium for output is the lineprinter. As we have just seen we can use graphic type devices to produce graphs, unusual alphabets and cine films. The problem of input is much more difficult and two active areas of research are
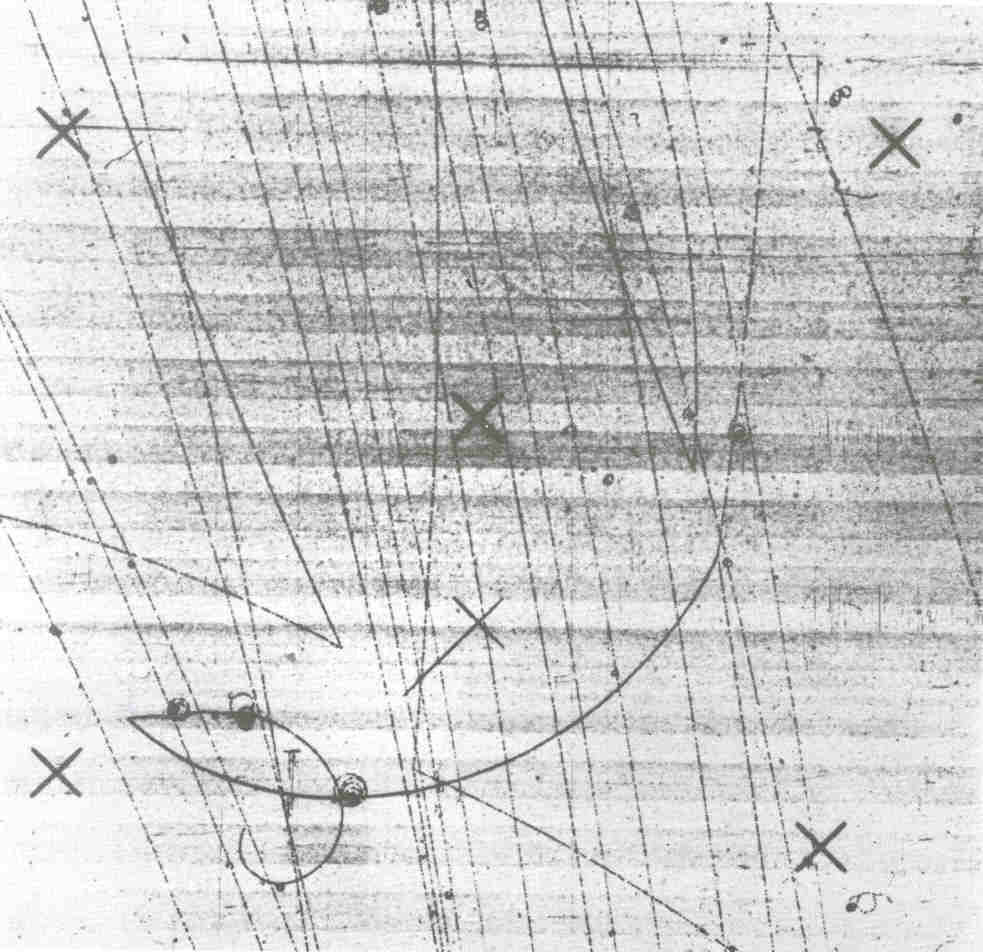
The former problem has been solved and is used for example in Bubble Chamber Track Analysis in High Energy Physics, but the equipment is still expensive.
The slides show bubble chamber tracks (Figure 3), and a girl adding extra information to a spark chamber track (Figure 4). The latter problem is partly solved but we still have a long way to go before such equipment becomes a common feature of all computer centres. When OCR equipment becomes readily available the use of computers in literary work will grow very rapidly.

An even more recondite problem is that of speech input to a computer. Research has been done on this but getting a computer to recognise commands given by even one operator is very difficult and I know of no one who has succeeded in doing much more than this.
Speech output from a computer is less difficult to achieve if we are content with the computer playing pre-recorded messages through an amplifier when it is instructed to do so. If however we want the computer to attempt to pronounce words which are typed in or generated by itself, we have a problem of a different order of magnitude.
At the IBM Research Laboratory at La Gaude, near Nice in the South of France, they have been working on this problem for some time. I was able to visit them in September 1970 and was very impressed with their work. Their approach has been as follows. They analysed the waveforms produced on an oscilloscope when a number of excellent speakers read passages of text containing a representative set of syllables; they used both men and women speakers and a variety of languages, including French and English. They then digitised the characteristic waveforms for each syllable (for those interested each syllable requires about 1,000 bits of information) and built into the program information relating to rules of pronunciation since the pronunciation of a syllable depends on the syllables close to it.
To test their system we were invited to sit at a typewriter console and type in any words, including our surnames, that we wished. We typed a long string of names and the computer spoke these very clearly - though with a French accent.
As an application of the system IBM then invited us to type in an announcement such as might be made at an airport, e.g. Alitalia announce the departure of their flight AL157 to Rome ..., etc., etc. The machine then spoke these messages quite beautifully.
IBM have very kindly sent me a tape of some such machine spoken messages preceded by the machine's pronunciation of a few random names ... You will hear the names and then the announcements concerning 2 flights in French and English. Remember when listening that these are not pre-recorded messages and the voices you hear are not those of any living person; they are entirely synthetic.
The title of my chair is Computing Mathematics and my own particular research interests lie in computers in Pure Mathematics and in information retrieval. I said earlier that Pure Mathematicians have so far not been among the most active computer users. I will therefore say something about computers in Pure Mathematics.
A study of the works of some of the greatest mathematicians of the 19th and 20th centuries, particularly Euler, Gauss, Jacobi and Ramanujan shows how willing they were to study numerical evidence in order to deduce a theorem. Having obtained evidence in favour of the theorem they would then set about proving it. As instances of this one can cite Euler's discovery of the continued fraction for ex, Gauss's discovery of the prime number theorem and of the law of quadratic reciprocity, Jacobi's fundamental formula in elliptic functions and Ramanujan's discovery of the congruence properties of the partition function.
Having seen this evidence I have no doubt that if these great men were alive today they would be active users of the computer. There is indeed some evidence supporting this view. Jacobi on one occasion visited Babbage and discussed his computing engines with him, showing great interest.
The branches of pure mathematics where computers are likely to be most effective are those branches dealing with discrete entities (such as integers) rather than those in which continuity and limiting processes are of great importance. Thus the obvious branches for computer applications are the Theory of Numbers, the Theory of Groups and Combinatorial Theory.
In the past few years a number of mathematicians have used computers to discover really worthwhile new results in these areas. Unfortunately most of them would take too long to explain but I can give you just a glimpse of two of the simplest cases: my own discovery of the congruence properties of the binary partition function 3 took only a few seconds of machine time and some effort on my part and yet these properties had not been noticed before even though Euler had first studied the function two hundred years ago.
Euler is also connected with my second illustration. You will no doubt recall from school days that the Diophantine equation x2 + y2 = z2 has the solutions (in integers)
32 + 42 = 52
52 + 122 = 132
and there are an infinity of other solutions. It is an unproved conjecture that there are no solutions in integers to the higher degree equations
xn + yn = zn, n≥3
(this is Fermat's Last Theorem which has been awaiting proof since 1639). Euler generalised this to the
There are no integer solutions to
x1
n + x2
n + ...+xn-1
n = xn
n for n≥3
The Conjecture is known to be true when n = 3 but nothing was known about n = 4, 5, ... until 1966 when a computer found that
275 + 845 + 1105 + 1335 = 1445
thus disproving Euler's conjecture which had stood for 200 years.
I must stress that I am not proposing that computers should be used for theorem proving, for I'm not at all optimistic about the prospects of proving anything worthwhile in a finite time. My philosophy is that a mathematician should use the computer to discover the theorem and then set about finding the proof himself.
Computers are being applied in many other areas ranging from art and music to the control of industrial processes and a wide variety of tasks in hospitals. Some of these applications are still at the pioneering stage, a few have foundered on problems of great difficulty whilst others have been very successful. The use of computers in medicine, for example, is, I think, still at the pioneering stage. The use of computers in language translation has met with limited success. Few people were surprised at this: the grammar, syntax and semantics of natural languages do not have a very rigorously defined structure. It is, of course, feasible to produce a program to translate one language into another at first-form level but to go much beyond this calls for a vastly greater effort. There are some delightful tales of computers producing schoolboy translations, thus there is the story (probably apochryphal) that the New Testament quotation The spirit is willing, but the flesh is weak was translated by one computer into Russian and retranslated by another computer into English, finally emerging as The vodka is holding out but the meat is poor. A more credible example is that the English phrase hydraulic rams was translated into another language as water sheep. There are however some very good machine translation programs and I would point to the Italian to English program written by Terry Crawford at University College, Cardiff as one of the best I've seen. (See figure 5).
Computers have been used to plan the choreography of a ballet, to produce drawings, paintings and even sculpture. They have composed music in the styles of Mozart, Bach, Haydn and Schoenberg as well as in styles unlike anything ever heard before.
I must admit that I have yet to hear a piece of computer-composed modern music that I find attractive; on the other hand, it is also true that I find very little human-composed modern music attractive either. Computers have been used to write children's stories, Westerns and modern poetry; in every case each individual line or sentence is very convincing but there is no real connection between one line and the next. So far only human beings can think up consistent, connected plots of any length.
At game-playing computers have been quite successful. They can match anyone at noughts and crosses or NIM and play games such as KALAH very well. Draughts appears to reach about their physical limit and a computer in 1962 beat an American master of the game, the first game he had lost in 8 years. Chess is so much more difficult that no computer has yet reached international standard although several have played at County class. I don't know of a computer playing Bridge or Poker but it would not surprise me to find one playing either game quite well.
Among the successes of computers, we must obviously count space research, weather-forecasting, molecular biology and a vast amount of less glamorous scientific research. As a very recent example the prediction of the existence of a 10th major planet of the solar system deduced from perturbations of the orbits of Halley's, Olbers and Pons-Brook's comets would, we are told, have taken about 20,000 years of calculation by hand, but was achieved in 100 hours by computers. The day will come, I am sure, when a computer will assist a human being to score a really notable success in the Arts, for example the decipherment of an unknown language such as Linear A. In the work on the Junius letters I think we have a foretaste of things to come in the literary field.
Among problems of outstanding difficult I would suggest that of producing a computer model of the economy of a country. Modelling of a large scale purely physical system such as the weather, can be difficult but is sometimes feasible and successful but this is a problem of a different dimension. Nevertheless I think it is a problem which ought to be tackled.
Another interesting but very difficult project is that of programming a computer to design a computer which is superior to itself. Although this sounds like science fiction I think it might one day be done. There are, of course, those who tell us that computers will be able to match man in any intellectual activity. Such statements are, in my view, naive in the extreme and almost as foolish as the views of the opposite group who foresee computers taking over the world, ignoring the fact that to stop a computer one need only switch off the electricity.
Computers make wonderful slaves. They prefer to work 24 hours a day, 7 days a week. Indeed they are more likely to go wrong after a few days rest than at any other time. They don't argue, rarely make mistakes even when carrying out the most tedious tasks, don't ask for overtime and don't pollute the atmosphere. They are millions of times faster at calculation than we are but they have no intelligence at all; if we ask them to do a stupid thing they do it at once, without question. The tiniest living creature has infinitely more intelligence than a computer is ever likely to have. The computer by itself is just a collection of electronics and mechanical devices, but as an aid to man's intelligence it represents one of the most significant advances in history.
I now return to the two questions I left unanswered near the beginning:
I hope that I have illustrated that computing is applicable to a very wide class of subjects and not just to engineering and physics. This fact was recognised by a Government Committee [5] two years ago which recommended that all undergraduates should be taught computing. I interpret this as meaning that a sufficient number and variety of courses should be available so that any undergraduate of any faculty who wishes to learn something about computing may do so.
In order to satisfy this need several levels of courses are required. At the most basic level there is a need for non-examinable programming courses which need to be differently oriented for science, arts, and social science students. At the next level there is the Part 1 course such as we introduced last year in combination with statistics or applied mathematics in the Faculty of Science. These courses have proved very popular and I was delighted when the Physics Department suggested the new combined Part I course Computing/Solid State Electronics which we shall be offering from next October.
For 2nd and 3rd year students there is the full Computing option in the Honours Mathematics or General Degree which follows the Part I course. Our first students will be starting this part of the course next October. These options are intended for students who are seriously interested in computing as a career.
Science students in Cardiff are now fairly well catered for in computing but we have yet to see what we can do for students in other faculties. Computing is, I believe, possibly the greatest inter-disciplinary subject to be taught in Universities. It blends naturally with a number of subjects such as statistics and electronics but is relevant to many more. The essentials of programming can be learned by any intelligent person in a few hours but herein lies a danger. We must always remember that computer time is very valuable, typically about a hundred pounds an hour and a programmer who is badly trained can waste thousands of pounds quite easily. If we are not to produce second rate programmers they must be taught professionally by people who keep up to date in all aspects of computing. At the same time they must not lose touch with the applications of computers in their own subjects. Thus one is led to the conclusion that the basic training should be done by the Computing Department, the applications being provided by the specialist departments later. Close collaboration between the Computing and other departments is clearly essential.
My aims then can be summarised in two sentences:
(1) Jean E. Sammet: Programming Languages: History and Fundamentals. Prentice-Hall Inc. (1969).
(2) Alvar Ellegard: "Who was Junius?" Almquist and Wiksell, Stockholm, (1962).
(3) R.F. Churchhouse: Congruence Properties of the Binary Partition Function. Proc. Camb. Phil. Soc. 66 (1969),371-375.
(4) L.J. Lander, T .R. Parkin: A Counter-example to Euler's Conjecture on Sums of like Powers. Bull Amer. Math. Soc. 72 (1966),1079.
(5)"Teaching of Computing in Universities". A report of a Joint Working Party. H.M.S.O. (1970).